<Ch8. 개요>
- Cluster analysis: 군집 분석
- Partitioning methods: 부분 나누기 방법
- Hierarchical methods: 계층적 방법
- Density-based and grid-based methods (밀도 기반, 격자 기반 방법)
- DBSCAN : high density(높은 밀도)를 가진 connected regions(연결된 지역)을 기반으로 한 density-based(밀도 기반) clustering
- DENCLUE: density distribution function(밀도 분산 함수)에 기반한 clustering
- Grid-based method - Evaluation of clustering (클러스터링의 평가)
<Density-Based Clustering Methods>
- density(밀도)에 기반한 Clustering
- 밀도의 척도: local cluster criterion 지역적인 밀도 기준(density-connected points 같은)
- ex: 밀도가 기준 이하 → 끊어져 있음 / 밀도가 기준 이상 → 이어져 있음 - 주요 특징들
- 임의의 모양인 clusters를 발견
- noise 처리
- 스캔 1번을 통해 밀도를 평가함. (이때, 데이터의 전체 분포가 아닌 특정 지역(로컬 영역)만을 봄)
- 클러스터링을 멈추기 위한 조건으로 density parameter가 필요함 - DBSCAN 알고리즘이 유명
<DBSCAN: Density-Based Spatial Clustering Algorithm with Noise>
- data 속에서 임의의 모양을 가진 clusters 발견
: 밀도 기반 공간 클러스터링 알고리즘으로, 데이터를 밀도(주변에 얼마나 많은 데이터가 있는지)에 따라 클러스터로 묶는 방법. - noise를 잘 처리함.
- 일반적인 클러스터링 알고리즘(예: K-Means)은 구형(원형) 클러스터를 잘 찾지만, 복잡하거나 자유로운 모양의 클러스터는 잘 못 찾음. → 하지만 DBSCAN 같은 밀도 기반 클러스터링은 "arbitrary shape"의 클러스터를 찾을 수 있음.
- 클러스터의 density-based 개념
- density-connected points(밀도 기준으로 연결된 점들)의 maximal set(더이상 확장할 수 없는 집합)으로 정의됨.
- Eps (ε): 이웃의 최대 반경
- MinPts: point의 Eps-이웃 안에 있는 points의 최소 개수 (threshold) - point q의 Eps(ε)-neighborhood
- NEps(q): { D에 속해있는 p | dist(p, q) ≤ Eps } → 집합으로 나옴
- p와 q의 거리 < Eps인 D에 속해있는 p (q의 neighborhood)
- |NEps(q)| : Eps 내에 들어오는 data points의 개수 - Eps 거리 내에 point 개수 ≥ Minpts → Dense 하다.

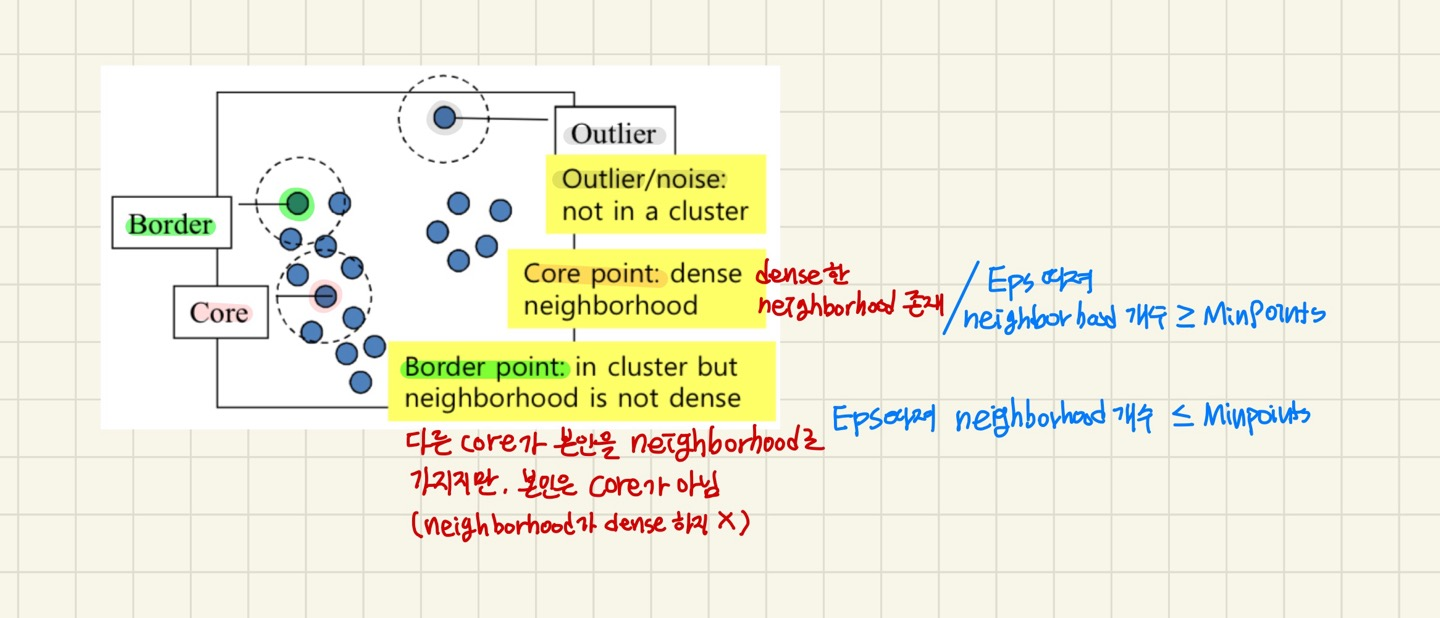
- Core : neighborhood가 dense함.
- Border: 다른 core가 본인을 neghborhood로 가질 수 있음. 그러나 본인은 core가 아님 (neighborhood가 dense하지 않음)
- Outlier: 그 누구의 neighborhood가 되지 않는 points, 본인도 neighborhood가 없음.
<DBSCAN: Density-Reachable and Density-Connected> (밀도-도달가능성과 밀도-연결성)
- p와 q의 연결성
- Directly density-reachable:
- p가 NEps(q)에 속해있음
- |NEps(q)| ≥ Minpts 면. q가 core이면
- point p가 Eps(ε)인 point q에 대해 directly density-reachable이다.
- unsymmetry

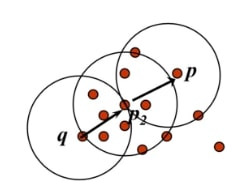
- Density-reachable:
- p1,...,pn, p1=q, pn=p인 points의 chain이 있음.
- p_i+1이 pi에 directly Density-reachable이면 (chain 형성)
- point p는 point q에 density-reachable이다.
- p, q는 반드시 core 여야 함.
- unsymmetry 함
- p와 q는 서로 neighbor가 아니다. 다른 core들로 연결되어있다.
- Density-connected:
- p와 q가 Density-connected하다는 것:
- Eps와 Minpts에 대해 p가 o로부터 density-reachable하거나
- q도 o로부터 density-reachable해야 함.
- p와 q가 core가 아닐 수 있다.

- 여태껏 k-means, agglogative, divisive, CFtree는 distance 기반 (가까운 것이 우리편)
- Density-based: 연결되어있으면 우리 편
<DBSCAN: 알고리즘> - 모든 data points를 core test함
1. 임의의 point p를 선택한다.
2. density-reachable인 모든 points를 찾는다.
3. p에 대해 Eps와 MinPts를 따졌을 때
- p가 core라면, cluster가 형성됨
- p가 border point라면, directly density-reachable points도 없고, DBSCAN은 DB의 다음 point를 방문한다.
- cluster 중 core가 아닌 것을 test
- core test를 하면 할수록 cluster가 확장되면서 신규 neighborhood가 유입됨. 자라나지 않을 수 있음(border or outlier)
4. 모든 points의 core test를 진행할 때까지 1~3을 반복한다.
참고: https://trivia-starage.tistory.com/156
- 계산 복잡도: 효율적인 공간 index(tree)가 사용된다면, O(nlogn) (n: DB objects의 개수)
- n*(core test 비용)
- 최악의 복잡도: O(n^2) - data points를 하나하나 다 test
- 기존의 kmeans: 가까운 것만 묶으려고 해서 cluster가 자세히 안 나올 수 있음.
- DBSCAN: 직관적으로 묶을 수 있다. but 하이퍼파라미터에 취약함. Eps, MinPts를 어떻게 잡느냐에 따라 결과 달라짐.
- 하이퍼 파라미터를 좋게 정하는 방법론은 아직 없음. try&error를 통해 정해야 함. - distance 가까운 것을 묶을지(k-means), connected된 것을 묶을지(DBSCAN) 정하는 것은 개인의 몫
<CLIQUE: Grid-Based Subspace Clustering>
- 2가지 이상의 알고리즘이 합쳐져서 새로운 알고리즘을 생성하는 예시
- 'subspace' 표현: 전체 dimension 중 일부의 dimension만 쓰겠다는 뜻
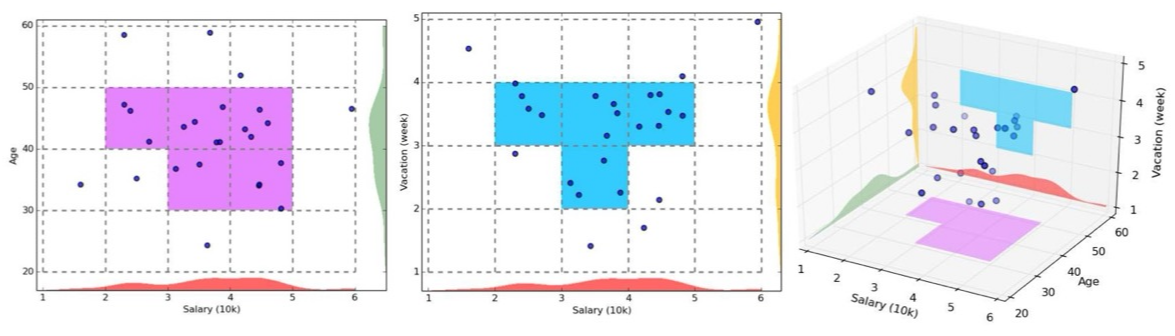
- CLIQUE: density-based, grid-based, subspace clustering 알고리즘
- 언제 쓰는가: dimension이 많을 때 효율적(dimesion이 많으면 거리 멀어짐, 차원의 저주에 빠지기 때문)
- Grid-based
- grid를 통해 data space를 discretize(*이산화) 함. (data points를 grid로 나눠서 grid 내에 있는 것을 같은 값으로 바꿈)
- grid cell 안 points의 개수를 세어 밀도를 측정 - Density based
- cluster: dense units(연결된 밀집 단위)의 최대 집합
- unit: unit에 포함된 data points의 비율이 입력 모델 매개변수(기준값)을 초과할 때 dense(밀집)하다고 간주. - Subspace clustering: 부분 공간 클러스터링
- Subsp ace cluster(부분 공간 클러스터): 임의의 부분공간에서 neighboring dense cells(이웃하는 밀집 셀)의 집합
- cluster에 대한 minimal descriptions(최소 설명)을 발견함.
- Grid-based
- CLIQUE 특징:
- Apriori principle을 사용하여 원래의 space보다 더 나은 클러스터링이 가능한 high dimensional data space의 subspace를 자동으로 식별함.
<CLIQUE: Apriori 가지치기를 이용한 Subspace clustering>
- Apriori 알고리즘 원리가 쓰임
1. grid cell 안 data points의 수를 세어 density(밀도)를 측정
2. threshold(minimum)에 의해 밀도가 낮은 것은 버림.
3. 다음 dimension과 조합해서 진행. 더이상 frequent한 것이 나오지 않을 때 or dimension 다 쓸 때까지
(* 이산화: 연속적인 값을 불연속적으로 바꿈. 1.01, 1.001, 1.0001 → 1)
4. 살아남은 것: frequent itemset이므로 여기서 max pattern이나 closed pattern만 봄.
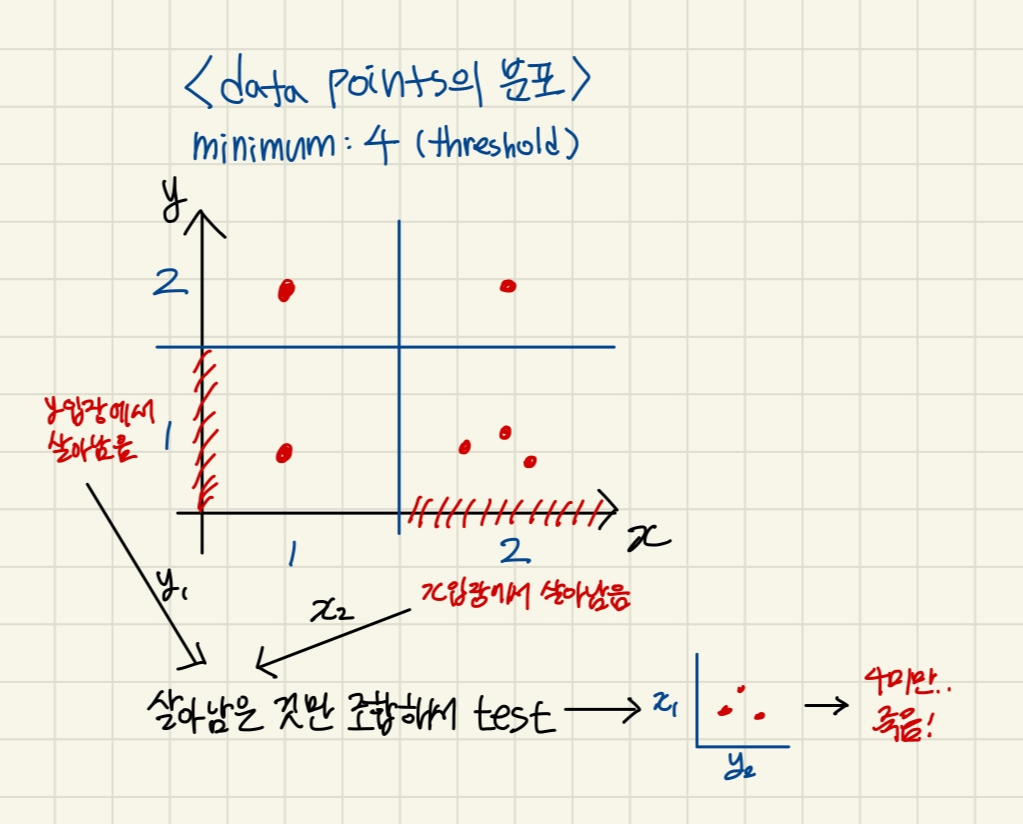
- ex) dimension이 10개인 것이 있다.
각 dimension마다 discretization 시킴 → discretization된 구간 내에서 threshold 미만으로 있는 구간 버림
→ 살아남은 구간을 이용해 2개의 구간씩 combination 구함 → 1~10 dimension까지 늘려가면서 살아남는 구간의 조합이 나올 때까지 진행
- 각각의 support ≥ 조합한 support
ex) 각 y1의 support: 4, x2의 support: 4 ≥ y1, x2 조합의 support: 3
<Clustering의 장점이자 단점>
- unsupervised learning: 정답을 모름.
장점인 이유: 준비 시간이 적음 (classification 같은 경우, supervised라 정답 작업을 진행해야 함)
단점인 이유: 정답이 맞는지 모름. 평가하기가 어려워진다. → Evaluation clustering (클러스터링 평가)이 진행되는 이유
평가를 진행해야 다른 방법으로 재시도 할지, 클러스터링을 멈출지 결정됨 (try&error 할지 말지)
<Evaluation of Clustering>
- cluster 내부는 유사도 크게, cluster끼리 (외부) 차별성이 크게
- 데이터셋에 사용한 clustering anlaysis 방법이 얼마나 적합한지 평가
- 특정 clustering 방법으로 나온 결과의 품질을 평가
- data structure(특성)을 잘 표현하는 clustering 결과를 얻을 수 있도록 함
ex) 영어 data를 가지고 clustering할 때, 모국어에 대한 정보에 따라 clustering이 됨 - 모국어가 내재된 원인이 됨
그러나 모국어 정보처럼 내재된 원인이 없을 수도 있다
- Clustering 경향성:
- clustering의 적합성 평가 - data에 내재된 grouping structure(그룹화 구조)가 존재하는지 확인 - Clustering 개수 결정:
- 데이터셋에 적합한 cluster 수를 결정
- 올바른 cluster 수를 찾아야 좋은 품질의 clustering 결과를 얻을 수 있음 - Clustering 품질 평가:
- clustering 결과의 품질을 평가한다.
- 결과가 data structure을 얼마나 잘 반옇하는지 판단
<Clustering Tendency: data가 내재된 grouping structure을 가지는가>
- data의 적합성 평가하기:
- data가 inherent grouping structure(내재된 그룹화 구조)를 가지는지 평가
- 내재된 그룹화 구조 = 비랜덤 구조 → 의미있는 cluster를 생성할 가능성을 보여줌
- Clustering Tendency(Clusterability) 결정하기:
- Clusterability(클러스터력): data가 클러스터링 될 가능성
- 매우 어려운 작업 (Cluster의 정의가 다양하기 때문)
- Cluster 정의의 유형: partitioning, hierarchical, density-based, grid-based ...
- 특정 Cluster 유형을 고정하더라도, 데이터셋에 적합한 null model(무효 모델)을 정의하는 것이 어려움.
(무효 모델: 데이터가 랜덤하거나 구조화되지 않은 상태라고 가정한 기준 모델. 실제 data가 무작위 분포에서 벗어난 의미있는 패턴(클러스터)를 가지고있는지 평가 가능)
- Clustererability Assesment Methods (클러스터력 평가 방법)
1. Spatial Histogram(공간 히스토그램): data의 histogram을 무작위 샘플에서 생성된 히스토그램과 비교
2. Distance Distribution(거리 분포): data points 간 거리 분포를 무작위로 생성된 샘플의 거리 분포와 비교
3. Hopkins 통계: spatial randomness를 평가하기 위한 희소 샘플링 테스트
<Clustering Tendency(Clusterability) 평가: Spatial Histogram>
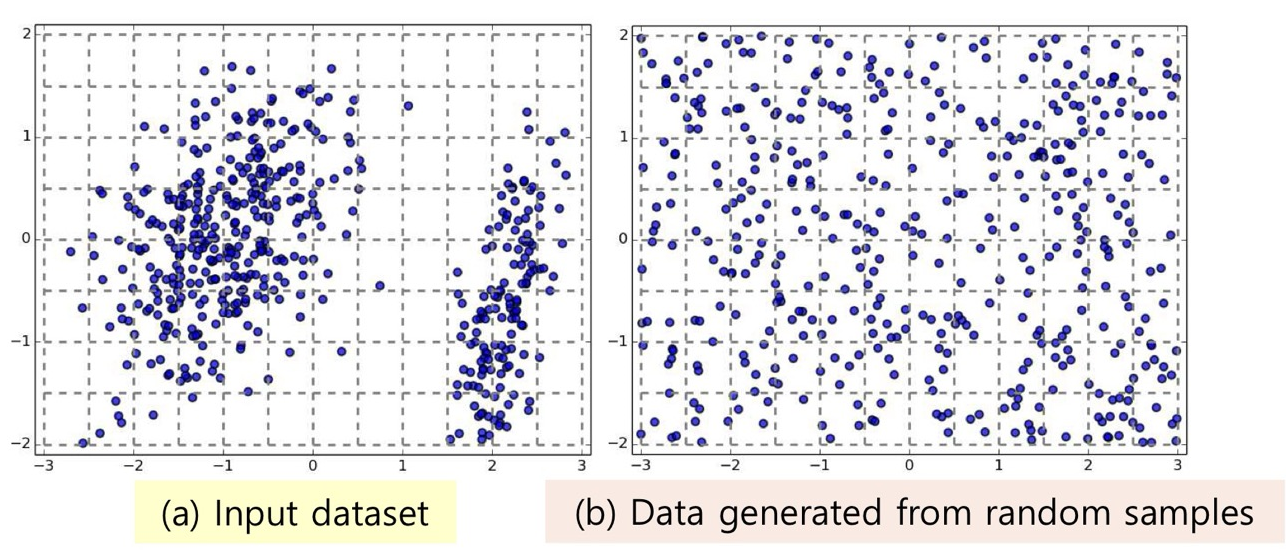
- 입력 dataset D의 histogram, random samples로부터 생성된 histogram을 비교
- EPMF 계산 이용한 비교법: 두 histogram에서 각 cell에 data가 존재할 확률 (각 cell 내 data points 빈도/전체 data points개수) → KL-Divergence를 써서 두 확률을 비교
- 두 확률이 유사: clustering이 잘 안 됨, 두 확률이 차이 남: clustering이 잘 됨
<Cluster의 수 결정하기: 1. 휴리스틱 이용>
- cluster 수의 양쪽 극단: 원하지 않음. 이 중간에 있는 개수 k를 원함 (아무도 k를 잘 모름)
- cluster의 개수가 1개: 1개로 뭉침
- cluster의 개수 = data의 수: 각각의 data가 집단을 가짐 - k를 정하는 휴리스틱(아래): 대략적으로 좋은 전략

ex) n=200, k=10 : data가 200개이면 10개의 cluster가 적당
- 한 cluster 당 몇 개의 data points가 존재하는 것이 좋은가?: 휴리스틱을 역수 취하기
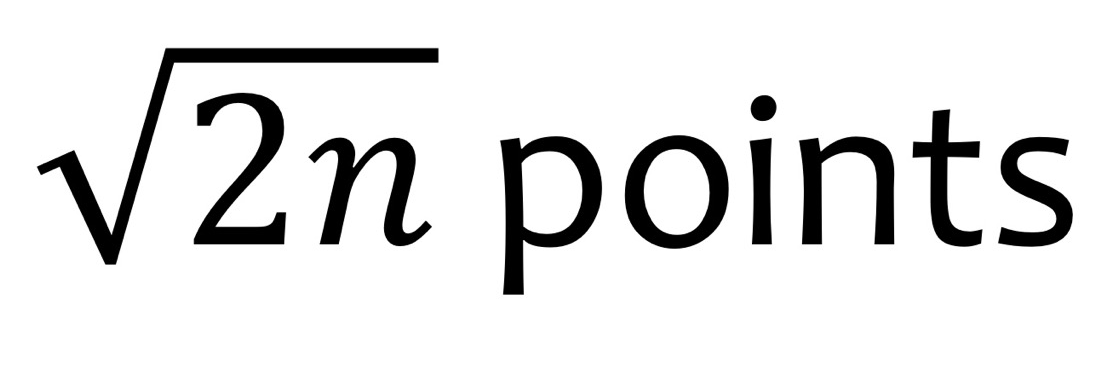
ex) cluster가 10개이면 data는 200개가 있는 것이 적당
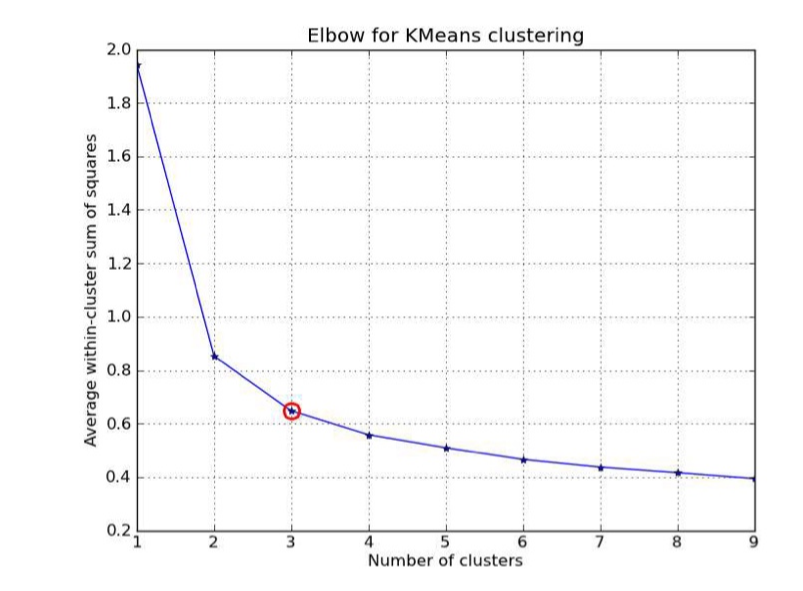
<Cluster의 수 결정하기: 2. Elbow Method> try&error
- cluster의 수의 분산을 그래프로 그림.
- cluster의 수가 증가 → 분산 값 감소
- cluster 1개: 분산 가장 높음, cluster 개수=data 개수: 분산이 0
- cluster의 유사도가 가장 높을 때, 쪼개면 분산의 감소량이 적음. (유사성 높은 것 끼리 나누면 분산값이 크게 낮아지지 않음)
- 감소량이 적어진 지점의 cluster 개수: 이 개수부터 cluster 내부의 동질성이 확보되었음
<Cluster의 수 결정하기: 3. Cross Validation Method> try&error
- elbow보다 try&error가 많음
- data를 m개의 부분으로 나누고, clustering에 m-1 부분을 사용한다.
- 남은 part(test셋)로 clustering의 품질을 test한다.
- 모든 data가 한 번씩 test셋이 되도록 m번 반복
- ex) m개로 나눴을 때, test셋의 각 point에서 가장 가까운 centroid를 찾음 → 그리고 test셋의 각 point에 가장 가까운 (본인이 선택한) centroids와의 제곱 거리의 합(SSD)을 구한다. → 제곱 거리의 합이 작을 수록 좋은 것(내가 속할 cluster를 정하고 잰 거리니까)
위를 m번 반복해 평균적인 값을 구함. clustering 모델이 얼마나 잘 작동하는지 확인
그것을 여러 k일 때와 비교해서 성능 평가함. 그 중에서 최적의 k값을 선택
<Clustering의 quality 측정>
- cluster 내부는 동질성이 높아지고, cluster 간은 이질성이 커져야 좋은 clustering이다.
- 동질성이 높은 것을 쪼개면 cluster간 이질성에 문제 생김. 이질성이 낮아짐 → 적절한 k가 필요한 이유
- 1번의 clustering 결과를 어떻게 평가할 것인가?
- Extrinsic vs Instrinsic
- Extrinsic(외재적 방법): Supervised(정답이 있음), 정답(ground truth)을 알고있다면 정답과 비교해서 평가함
- 클러스터링 결과를 이상적인 참조 클러스터링과 비교해 품질 측정 (precision, recall, F1-score..) - Intrinsic(내재적 방법): Unsupervised(정답을 모름), 어떻게 수치화 할 것인가. 앞에서 봤던 방법들이 이에 속함
- data 자체의 속성만 사용하여 평가: 클러스터 간의 분리가 잘 이루어졌는지(클러스터 간 거리 증가), 클러스터 내부가 얼마나 밀집되어있는지(클러스터 내부 거리 감소)
<Clustering 품질 측정하는 일반 기준: Extrinsic methods>
- 원칙: cluster 내부는 동질성이 높아지고, cluster 간은 이질성이 커져야 좋은 clustering이다.
- Cg: 이상적인 Clustering Ground truth (정답)
- C: Clustering 결과
- Q(C, Cg): clustering C에 대한 품질 척도
- Q(C, Cg)는 아래 4개의 필수 기준을 만족해야 함.
1. Cluster homogeneity: 더 pure할 수록 품질이 좋음.
2. Cluster completeness(완전성): 동일 category에 속하는 객체들이 동일 cluster에 배정될 수록 더 좋은 품질
ex) 같은 category의 object가 여러 cluster에 나뉘지 않고 하나의 cluster에 포함되어야 함.
3. Rag bag better than alien: 다 같은 것에 이상한 것 하나 넣는 것보다 다 다른 것에 이상한 것 하나 넣는 것이 좋음. 순수한 cluster가 깨지면 나쁜 품질. → 동질성 높은 clsuter를 보존하라
4. Small Cluster Preservation(작은 클러스터 보존): 작은 category를 나누는 것은, 큰 category를 나누는 것보다 더 해로움 → 작은 거 말고 큰 category를 나누자.
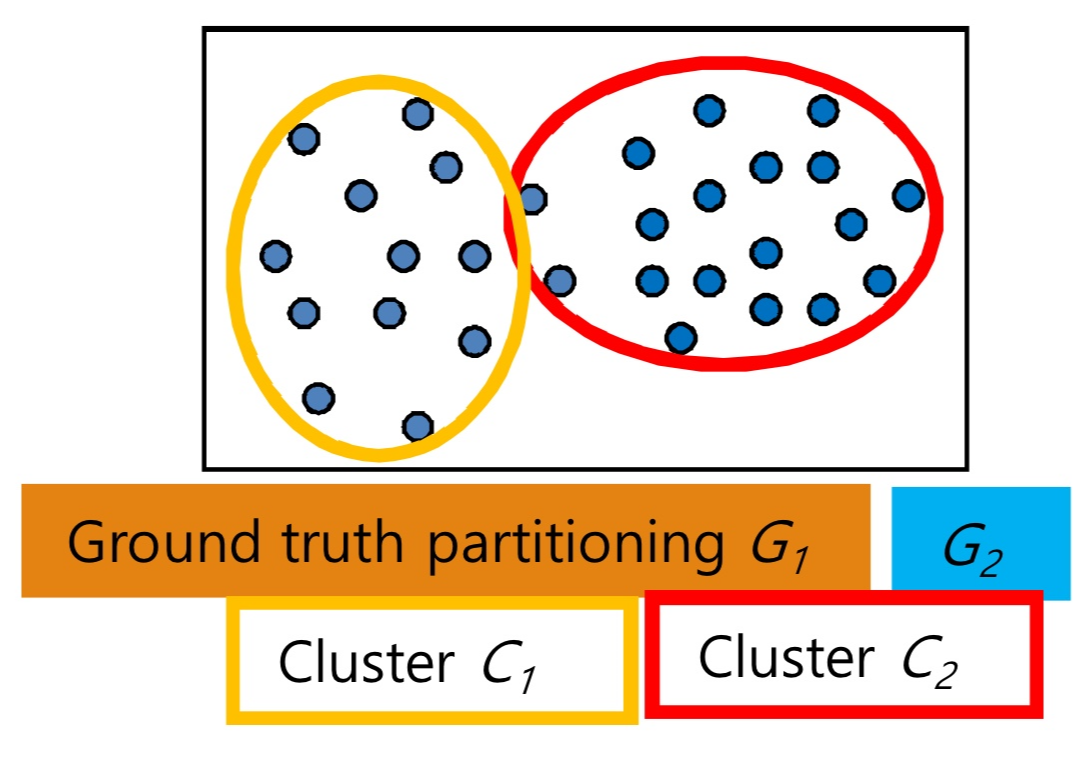
- Cg와 Clustering의 결과가 다르게 나왔음 → 맞는지, 틀린지를 어떻게 판단할까?
<Extrinsic methods: 1. Matching-Based methods>
- 내가 만든 알고리즘 clustering의 결과(C)와 참조 데이터(ground truth)를 비교헤 품질 평가.
- 내가 만든 Cluster: C={C1,C2,..., C_m} 데이터셋 D={o1, o2, ..., o_n}을 m개의 cluster로 나눔:
- Ground truth: G={G1, G2, ..., G_l} 데이터셋 D={o1, o2, ...,o_n}을 l개의 cluster로 나눔.
- 내가 만든 cluster 중 참조 데이터(ground truth)의 cluster와 교집합인 것의 비율
- cluster Ci의 Purity: cluster Ci에 포함된 ground truth 그룹 Gj의 점의 최대 개수를 Ci의 점의 개수로 나눔. |Ci∩Gj|
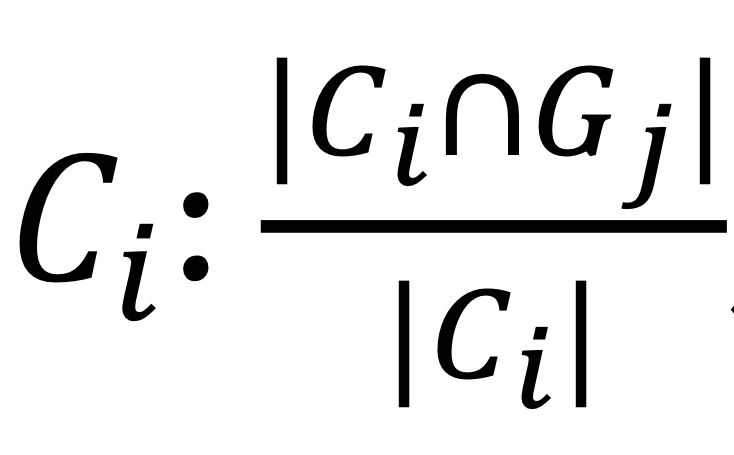
- clustering C의 total purity: 각 cluster Ci에 포함된 Gj 점의 최대 개수( |Ci∩Gj| )를 다 더해서 datasets의 개수(n)으로 나누기.
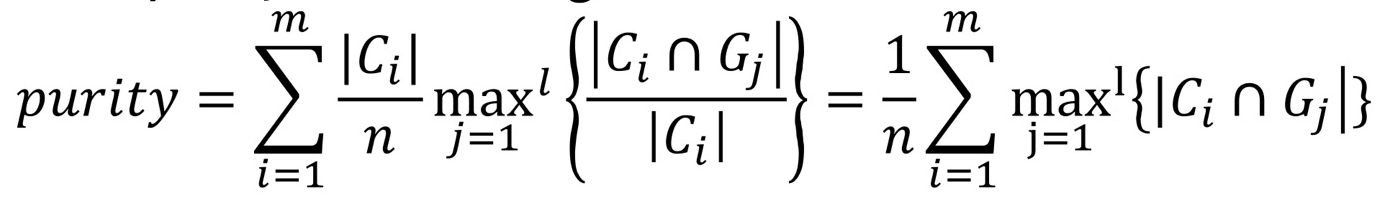

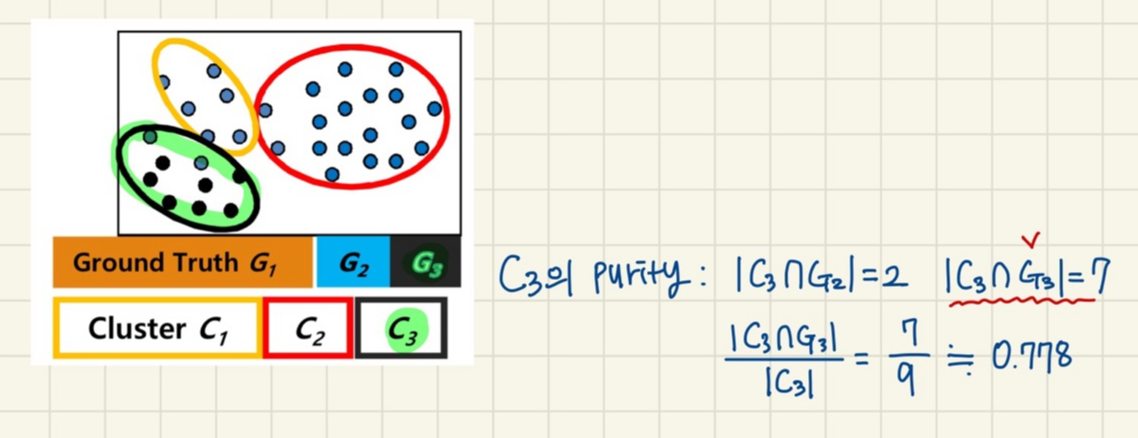
- Matching-Based Method 예시
- 11 objects
- 각 cluster Ci에 포함된 Gj 점의 최대 개수( |Ci∩Gj| )의 총합 / datasets의 개수(n)

<Information Theory-Based Methods 1. Conditional Entrophy 조건부 엔트로피>
- clustering 결과가 Ground truth에 가까울 수록 더 적은 정보로 데이터를 설명할 수 있음 → 좋은 cluster
- cluster 내부의 동질성 높게, 즉 Cluster 내에는 1개의 Ground truth의 label만 모여있길 바람.
→ Entrophy(복잡도)가 낮을수록 good 동질성 - cluster 결과 Ci 내부에 존재하는 Ground truth의 label에 대한 entrophy 값을 계산.
- 각 cluster 결과 Ci 내부에 Ground truth가 존재할 확률
- clustering C의 Entrophy:
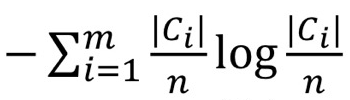
- Ground truth의 Entrophy:
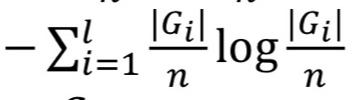
- Cluster Ci(개별)에 주어진 G의 Conditional Entrophy:
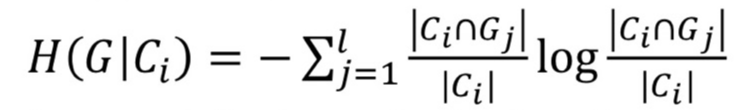
l: G의 최대 개수, j: l까지 증가하는 변수
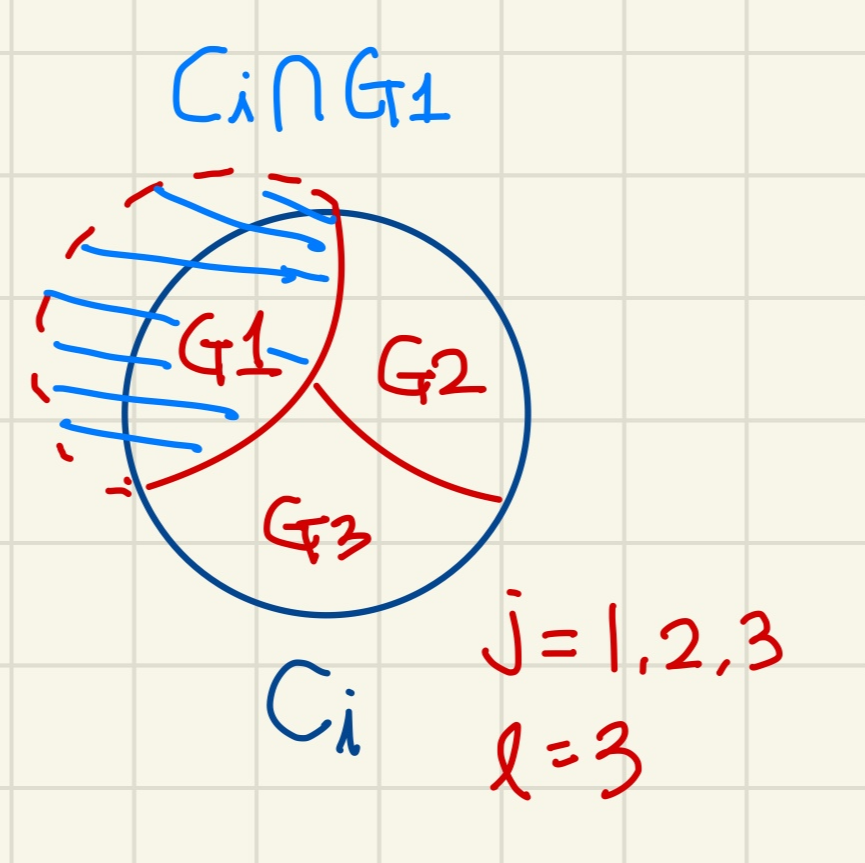
- Clustering C(전체)에 주어진 G의 Conditional Entrophy: C1~Cm까지 더함 (가중 평균)
- 낮을 수록 좋은 것이다.
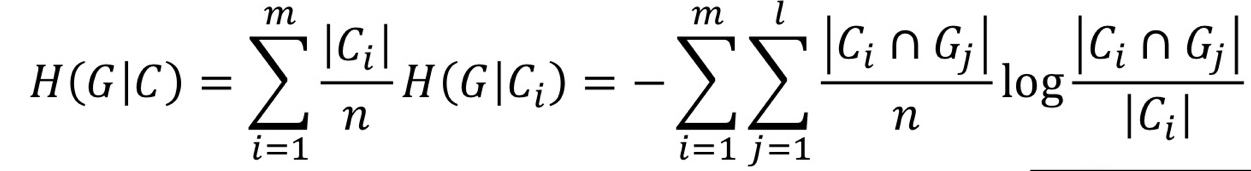
- 위 Conditional Entrophy는 동질성만 고려함. (이질성은 딱히 고려 X)
- Clustering C에 주어진 G의 Conditional Entrophy 예시:

<Information Theory-Based Methods 2. Normalized Mutual Information (NMI)>
- Mutual information I(C,G) :
- 2개의 분포가 있을 때 한 분포를 독립으로 고정해 놓고, 다른 한 분포를 측정했을 때 얼마나 차이 나는지
- Clustering 결과와 Ground truth가 관련이 없다고 설정. → 차이가 클수록 좋은 것이므로, NMI 값은 클수록 좋음.
- KL-Divergence와 비슷
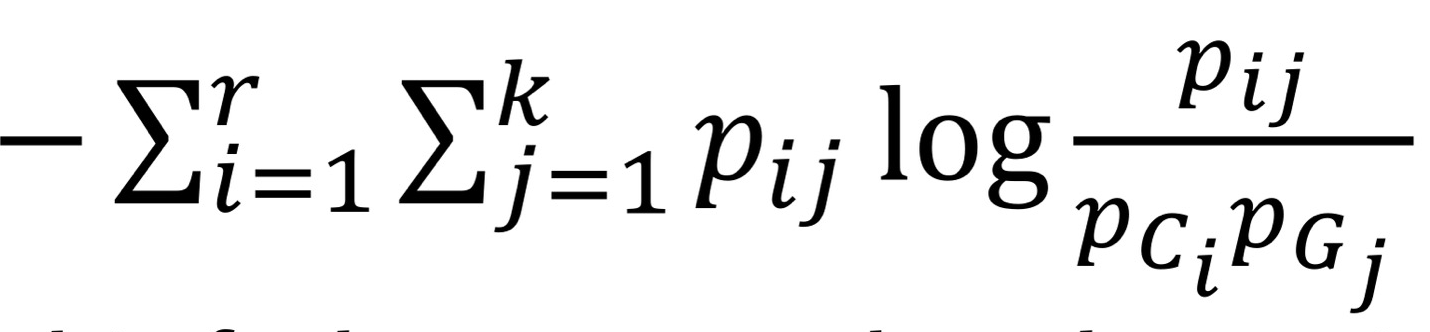
<Pairwise Comparison-Based Methods: Jaccard Coefficient>
- 데이터셋 D에 있는 모든 data 객체 쌍 (oi, oj)에 대해 clustering 결과를 평가
ㄴ = clustering이 끝난 임의의 data points 2개 (oi, oj)
1. Ground truth에서 같은 그룹, Cluster에서도 같은 그룹에 있음: True Positive (TF)
2. Ground truth에서는 같은 그룹이 아님, Cluster에서는 같은 그룹: False Positive (FP)
내 Cluster에서 긍정(P)이라고 잘못(F) 판단
3. Ground truth에서는 같은 그룹, Cluster에서는 같은 그룹이 아님.: False Negative (FN)
내 Cluster에서 부정(N)이라고 잘못(F) 판단
4. Ground truth에서 같은 그룹이 아님, Cluster에서도 같은 그룹 아님.: True Negative (TN)
- 모든 가능한 pair의 수 N = n(n-1)/2
- N개의 pair를 위 4가지 경우 중 1개로 간주할 수 있음.
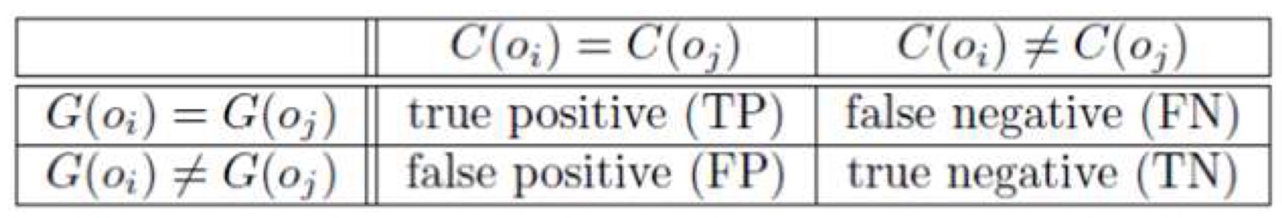
- Jaccard Coefficient: TN(True Negative) 무시, 나머지만 고려
Jaccard = TP/(TP+FN+FP) - Jaccard가 1에 가까울 수록 좋은 clustering. 1이면 완벽한 clustering
(C!=G인 쌍을 모두 무시했으니) - 여기서도 동질성만 고려함. 이질성 평가하지 않음.
<Intrinsic Methods: 1. Dunn Index>
- 정답(Ground truth)을 모를 때. Unsupervised
- 동질성과 이질성을 모두 평가 (cluster 간 동질성이 작고, 이질성이 커지길 기대)
- 동질성 평가: Δ , 같은 cluster 내에서 서로 간의 거리가 가장 먼 값 (값이 작으면 good)
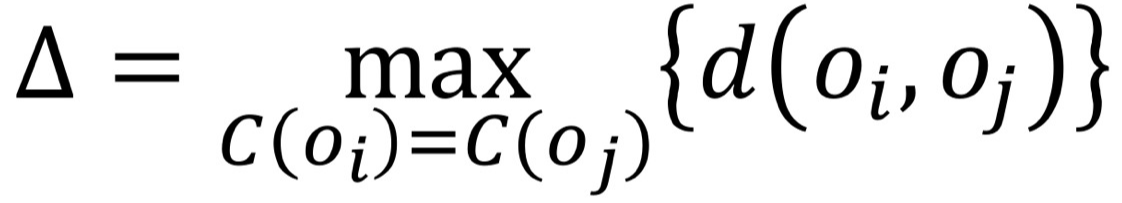
- 이질성 평가: δ , cluster 간 거리가 가장 가까운 값 (값이 크면 good)
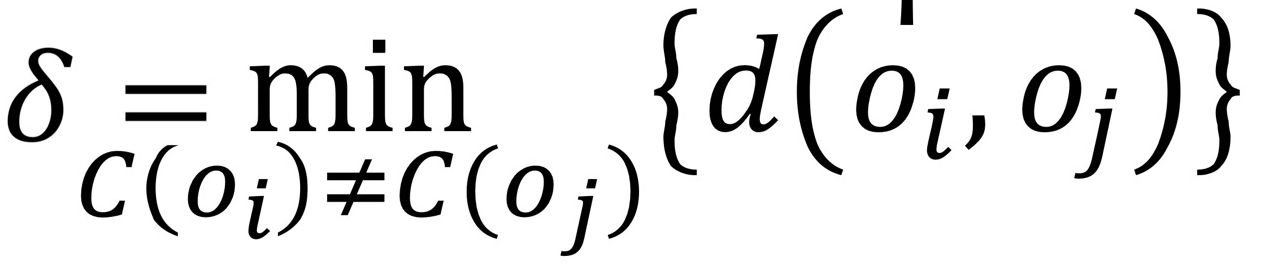
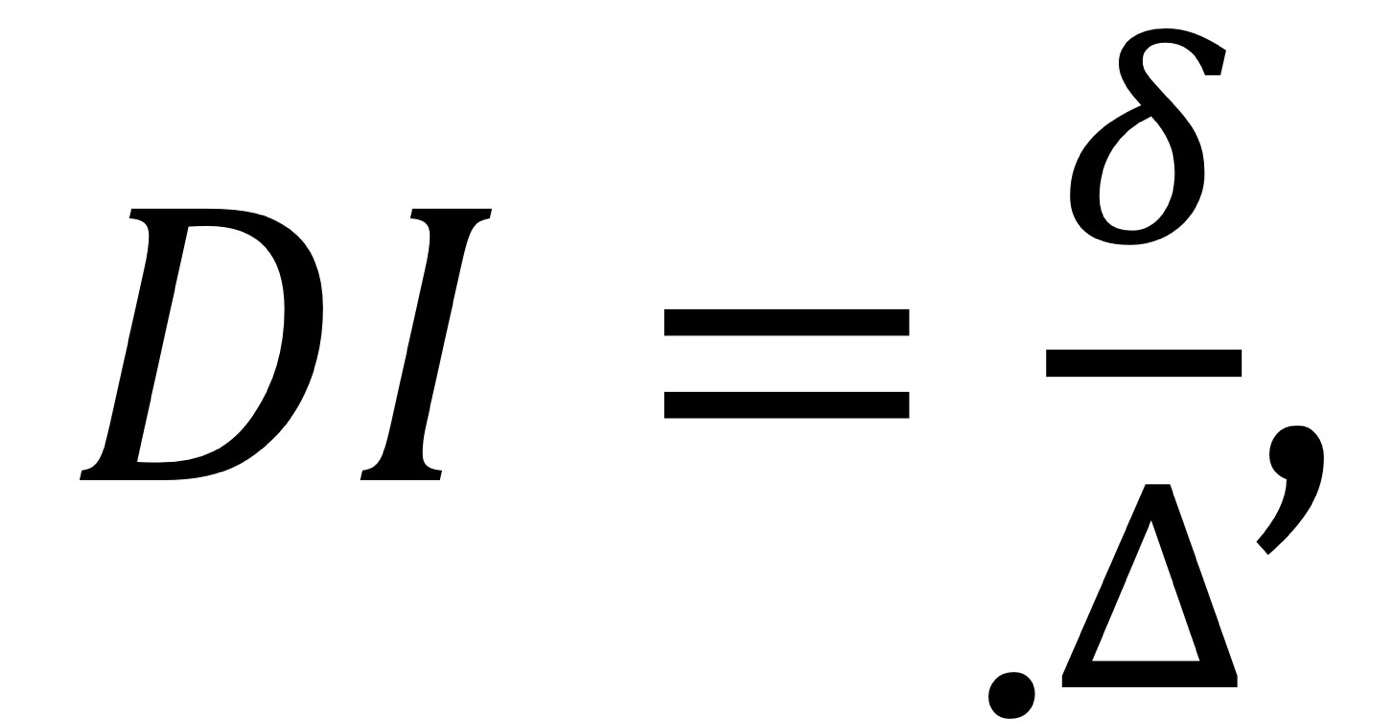
- DI의 값이 클수록 좋은 clustering
- but Δ 과 δ는 최대값, 최소값을 사용하므로 outlier에 취약함. → 그냥 distance의 평균을 구하자 (실루엣 계수)
<Intrinsic Methods: 2. Silhouette Coefficient(실루엣 계수)>
- 데이터셋 D가 k개의 cluster로 나누어져 있다고 하자: C1,...,C_k
- o: 자신, o': 다른 object, |Ci|: Cluster Ci에 속한 object 수
- D의 각 object o에 대해
- o와 o가 속한 cluster내 objects 사이의 평균 거리 a(o): 응집도(compactness)
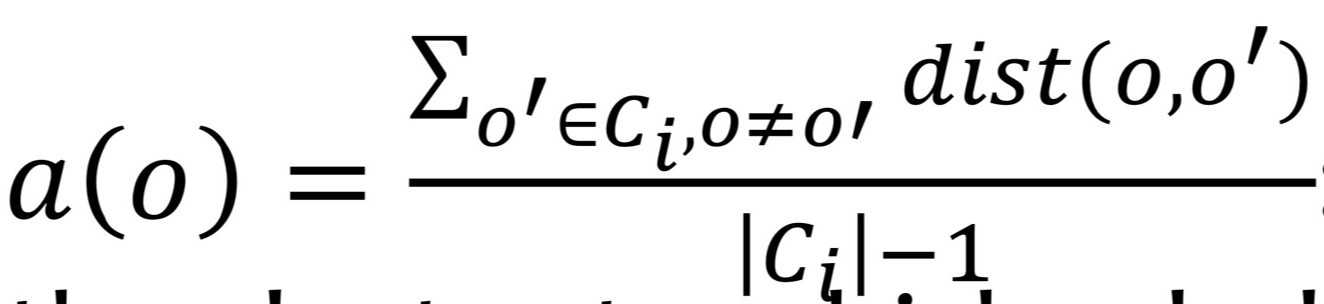
a(o) 값이 ↓ (내부 객체 간 거리 짧아짐) → 응집도 ↑
- o와 o가 속하지 않은 clusters들 각각에 대해 계산한 평균 거리의 최소값: 분리도(seperation)
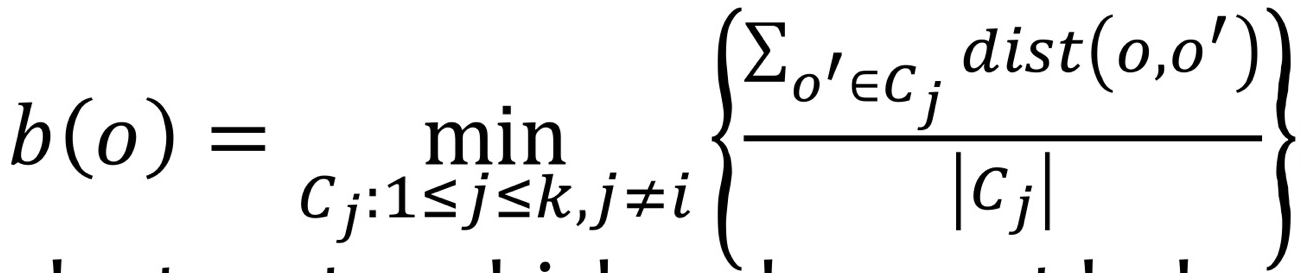
b(o) 값이 ↑ (cluster 간 거리 멀어짐) → 분리도 ↑
- Silhouette Coefficient:
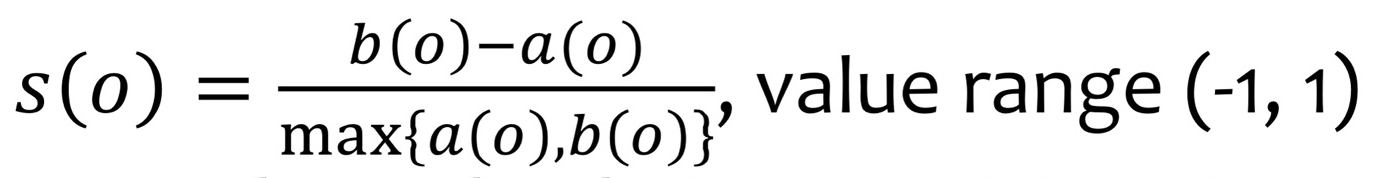
- 값이 1에 가까울 때: o가 속한 cluster의 응집도 ↑, 다른 cluster와 분리도 ↑, 이상적인 clustering
- 값이 0에 가까울 때: o가 여러 cluster의 경계에 걸쳐 있음. → clustering 품질이 좋지 않음.
- 값이 음수 (s(o)<0): o가 속한 cluster보다 다른 cluster에 가까움. → clustering 품질 매우 좋지 않음.
'공부 > 데이터 마이닝' 카테고리의 다른 글
| [데이터 마이닝] Ch11. Outliers - Statiscal, Proximity-based outlier detection (0) | 2024.12.01 |
|---|---|
| [데이터 마이닝] Ch11. Outlier - Basic concept (0) | 2024.12.01 |
| [데이터 마이닝] Ch8. Cluster analysis -Hierarchical methods (0) | 2024.11.20 |
| [데이터 마이닝] Data, Measurements and Data Preprocessing (0) | 2024.10.16 |
| [데이터 마이닝] Pattern Mining: FP-Growth (freq 패턴 마이닝) (0) | 2024.10.10 |