<Pattern-Growth Approach: candidate를 생성하지 않고 Frequent 패턴을 마이닝 하기>
- Apriori approach의 장애물(단점)
- Breadth-first search: 메모리를 많이 씀. 모든 것을 탐색해야 함. (비효율적)
- candidate를 생성하고 테스트함: 종종 많은 양의 candidate가 생김
- memory 안에 candidate가 다 들어가야 알고리즘 성능이 좋아짐. → candidate 개수가 줄어야 함. 어떤 case에는 메모리에 candidate를 다 넣을 수 없음 - 그래서 생긴 FPGrowth Approach
- Depth-first search
- 명확한 candidate 생성을 피한다.
- 원리: 지역 frequent items 만을 사용해서 짧은 패턴 → 긴 패턴으로 성장시킴
ㄴ frequent pattern인 "abc" / "abc"를 가진 모든 transaction들을 얻는다. (transaction = abc의 프로젝트 DB) /
"d"는 프로젝트 DB안의 local frequent 아이템이다. → abcd는 frequent pattern 이다.
<Transaction DB에서 FP-tree 만들기>
min_support = 3
1. DB를 1번 스캔하면서, frequent 1-itemset(single item pattern)을 찾는다. (misup 이상인 것으로 따져서 찾기)

2. 내림차순 frequency 순서인 f-list: frequent item들을 정렬한다. (Header Table 참조)

3. DB를 다시 scan하면서, (Global) FP-tree를 생성한다.
- TID 별로 (ordered) frequent items를 읽으며 {} 아래에 하나씩 tree를 내린다. 읽을 때마다 frequency 숫자를 1씩 늘림. tree 내리다가 새로운 알파벳이 나오면 새로운 가지를 만들어 그 알파벳을 내려줌.

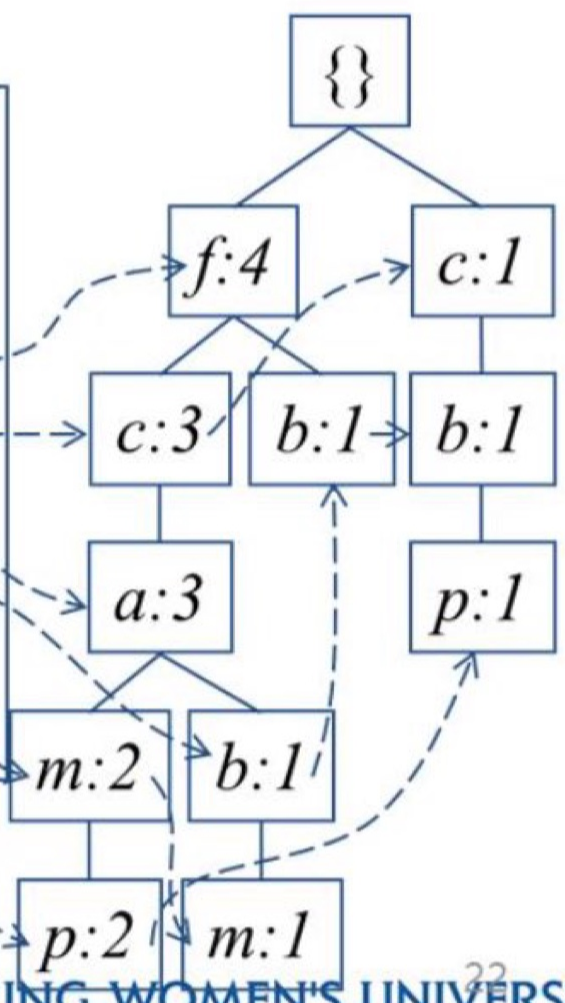
FP-tree 만들어 보았으니, FP-growth 과정을 계속 진행해보자.
<patterns과 database를 나누기>
- frequent patterns들은 f-list에 따라 집합으로 분할될 수 있다.
- F-list = f-c-a-b-m-p
- p를 포함하는 패턴들
- p는 없지만 m을 가진 패턴
- ...
- a, b, m, p를 가지진 않았지만 c를 가진 패턴
- f 패턴
- 완결성이 있고, 중복 없게 저장을 한다.
1. FP-growth: conditional pattern base 만들기
- FP-tree 내 가장 끝, 가장 frequent하지 않은 요소부터 시작한다.
(FP-Tree를 만들 때, 가장 빈도가 높은 요소부터 root에 집어넣는 것과 반대다.)
p conditional pattern base (p가 포함된 pattern)
m conditional pattern base (m이 포함되었으나 p가 포함되지 않은 pattern)
b conditional pattern base (b가 포함되었으나 p, m이 포함되지 않은 pattern)
....
f conditional pattern base (f가 포함되었으나, 나머지가 포함되지 않은 pattern) - frequent item p의 연결을 따라 아래에서부터 위로 FP-tree를 순회한다.
- item p를 따라 root까지 가면서 p의 conditional pattern base(조건부 패턴 기준)을 형성함.
- p는 제외하고 셈 (이미 포함된 것으로)
- p의 경우, p:2에서부터 시작해서 누적해서 m:2, a:2, c:2, f:2로 cond.pattern base에 fcam:2 존재,
p:1쪽에서 시작해서 b:1, c:1로 cond. pattern base에 cb: 1 존재. - 같은 방식으로 p,m,b,a,c,f 순서로 conditional pattern bases 생성

2. FP-growth: conditional pattern tree 만들기 (conditional pattern base로부터)
- 각 pattern-base에 대해
- 각 항목에 대해 frequnecy를 쌓아 나간다.
- pattern base의 frequent items에 대한 FP-tree를 생성
- 예시: m-conditional pattern base 만들기

- m과 관련된 모든 frequent patterns : {m}, {f, m}, {c, m}, {a, m}, {f, c, m}, {f, a, m}, {c, a, m}, {f, c, a, m}
- p-conditioanl pattern tree 만들기
- conditioanl pattern base랑 별로 관련 없어 보인다.
- 아닌가? base 표를 보면 두 패턴 중 겹치는 c가 있으니 그게 frequent로 작용하는 걸까

- p와 관련된 모든 frequent patterns: {p}, {c, p}
<각 conditional FP-tree로 Mining(패턴 분석)>
- m-conditional FP-tree에서 얻을 수 있는 사실: 연관된 frequent itemset의 conditional pattern base와 conditioanl FP-tree를 알 수 있다.


- 같은 DB에서, 최종적으로 Apriori가 찾은 frequent itemsets와 동일하다.
<FP-tree 구조의 장점>
- 완전성(Completeness):
- frequent pattern mining에 대해 완전한 정보(frequent itemsets)를 보존할 수 있다.
ㄴ DB를 2번만 scan하고, 그다음부터는 FP-tree만 본다.
ㄴ DB 압축해서 HDD에 올라가는 DB의 scan을 2회로 제한 → 성능 good
- transaction (각 data)의 긴 pattern을 깨지 않는다. - 압축성(Compactness)
- 관계 없는 정보는 줄인다: infrequent한 item들을 버린다.
- frequency 내림차순으로 정렬된 item들: frequency가 높은 것들은 패턴들이 share할 가능성 높음, tree에서 공유 많이 됨
root 가까운 쪽에 frequent한 것이 위치하면 subtree 사이즈가 감소한다. conditional FP Tree를 작게 만들기 위해 내림차순 사용
- 원래 DB보다 더 크지 않다: node-links를 세지 않고 field를 센다.
<Frequent Pattern Growth Mining 방법>
- idea: Frequent pattern growth(성장)
- DB partition(분할)과 pattern에 의해 frequent patterns를 재귀적으로 성장시킴 (읽었던 것 다시 읽고 또 읽고) - Method:
- 각 frequent item에 대해, 1. conditional pattern-base 생성, 2. conditional FP-tree를 생성
- 각 frequent pattern에 대해 새롭게 FP-tree를 만드는 과정을 반복
- FP-tree가 {}공집합으로 빌 때까지, 혹은 1개의 경로(path)만 남을 때까지 반복
ㄴ 1개의 경로(single path)는 굳이 만들지 않아도 됨. 각 모든 frequent pattern을 합쳐 조합한 것이다.
<FP-Growth vs Apriori>

- Support threshold 감소할수록(제한이 줄어드니) candidate 생성 증가. / Support threshold 늘수록 candidate 안 만들어짐
- candidate 생성이 증가할수록
→ Apriori Runtime 증가 (속도 느려짐, 성능 나빠짐)
→ FP Growth Runtime 감소 (속도 빨라짐, 성능 좋아짐)
<Pattern Growth Approach의 장점>
- 분할 정복 (Divide and conquer):
- 현재까지 얻은 frequent patterns에 따라 mining task와 DB를 분리한다.
- 더 소규모 DB에 초점을 맞춘 탐색으로 이끈다. - candidate를 생성하지 않아도 됨, candidate를 test하지 않아도 됨
- Database를 압축함: FP-tree 구조로
- 전체 DB의 scan을 반복하지 않아도 된다.
- 기본 작업: 지역 frequent items를 세고, sub FP-tree를 생성한다. 패턴 검색과 일치하는 것은 없음
'공부 > 데이터 마이닝' 카테고리의 다른 글
| [데이터 마이닝] Ch8. Cluster analysis -Hierarchical methods (0) | 2024.11.20 |
|---|---|
| [데이터 마이닝] Data, Measurements and Data Preprocessing (0) | 2024.10.16 |
| [데이터 마이닝] Pattern Mining: Pattern Evaluation Methods (1) | 2024.10.02 |
| [데이터 마이닝] Pattern Mining: Methods (Apriori) (1) | 2024.10.01 |
| [데이터 마이닝] Pattern Mining: Basic Concepts (1) | 2024.09.27 |