Data Types, Statics of Data, Similarity and Distace9 Measures, Data Quality, Data Clening and Data Intergration, Data transformation, Dimensionality Reduction, Summary에 대해 배워보자.
<Types of Data Sets>
1. Record Data (기록된 데이터)
- Relational records: Relational tables(관계형 테이블), highly structured(구조화된
- Data matrix ex. numerical matrix(숫자 배열), crosstabs (교차표)
- Transaction data (발생 데이터, 변동 데이터)
- Document data: Term-frequency vector(matrix) of text document (텍스트 문서의 frequent한 용어 벡터)

2. Graphs and Networks (그래프와 네트워크)
- 운송 네트워크
- World Wide Web
- Molecular structures
- Social or information networks(sns)
3. Ordered Data (순서있는 데이터)
- Video data: 연속적인 이미지 (sequence of images)
- Temporal data: time-series (시계열, 시간에 따라 기록됨)
- Sequential Data: 연속적인 transaction (transaction sequence)
4. Spatial, image and multimedia Data (공간, 이미지, 멀티미디어 데이터)
- Spatial data: maps (지도)
- Image data: 사진
- video data
<Structured Data의 중요한 특징>
- Dimensionality(차원수)
- 차원의 저주(차원이 많아지면 data 구별 어려워짐, 처리속도 증가) - Sparsity(희소성)
: 오직 존재하는 data만 count (없는 데이터가 많음. 데이터의 희소성) - Resolution(해상도)
: 패턴은 범위에 의존한다(범위(scale)이 다르면 다른 정보처럼 보임. 통일 시켜주기) - Distribution(분산)
: 중심성과 분산
<Data Objects>
- Data sets는 data objects로 이루어짐.
- individual한 data의 단위. 여러 dimesion의 정보를 저장 (dimesion = data object의 개수 = attribute의 개수)
- A data object는 entity를 나타낸다.
ex) sales database: customers, store items, sales (3차원)
medical database: patients, treatments (2차원) - Data objects = samples, examples, instances, data points, objects, tuples
- Data objects는 attributes(특성, 변수)에 의해 설명된다.
- Database rows(행) → data objects; columns (열) → attributes (변수, 특성)
<Attributes>
- Attribute ( = dimension, features, variables)
- data object의 특징이나 특성을 나타내는 data field
- ex) customer_ID, name, address - Types(유형)
- Nominal 이름, 명사(ex. red, blue)
- Binary (ex. 참/거짓 중 하나 1/0 중 하나)
: nominal인 true, false로 나타낼 수 있고, numeric인 1,0로 나타낼 수 있다.
- Ordinal (ex. {freshman, sophomore, junior, senior} 처럼 순서적 개념 존재.)
: nominal한 명사로 순서 (1,2,3,4...) 나타내므로 nominal과 numeric의 중간
- Numeric: 정량적인
: Interval-scaled: 섭씨 100도는 상대적이다. 곱셉 덧셈 어려움.
Ratio-scaled: 화씨 100도는 절대적이다. 곱셈 덧셈 가능.
- Discrete vs. Continuous Attributes
: Discrete - 일반적으로 Integer, 숫자를 더하는 것(모든 숫자의 합)
Continuous - Real Number. 두 수 사이에 무한 개의 숫자 존재. 면적값(integral)
<Attribute Types>
- Nominal(이름, 명사): categories, states or "어떤 것의 이름"
- 물질의 상태, 직업, ID 숫자, zip code 등
ex) Hair_color = {anburn, black, blond, brown} - Binary (2진, 2개로 이루어진)
- 2개의 상태(1, 0)를 Nominal attribute (True, False)로 나타낼 수 있음.
- Symmetric binary: 동등하게 중요한 outcomes. ex) gender
- Asymmetric binary
: 동등하지 않게 중요한 outcome. ex) medical test,
일반적으로 1에서 가장 중요한 outcome을 배정함 - Ordinal (순서를 가지는 것)
- 의미있는 순서(ranking)을 가지지만, 연속적인 값의 크기는 알려져있지않음
- size={small, medium, large}, 성적, 군대 계급
<Numeric Attribute Types>
- Interval (구간)
- 같은 간격으로 측정되는 값. 간격이 동일하다.
- 값은 순서를 가지고 있다. ex) 섭씨나 화씨, 날짜
- 영점이라는 개념이 없다. - Ratio
- 절대 영점이 존재한다.
- 크기 비교도 가능하고 차이와 비도 계산할 수 있는 데이터. 모든 연산이 가능한 변수의 척도.
- 절대 온도가 여기에 해당. ex) 5캘빈의 2배는 10캘빈이다.
<Discrete vs Continuous Attributes>
- Discrete Attribute
- 유한하거나 셀 수 있는 무한한 값의 집합. ex) zip code, 문서의 단어 집합
- 때때로 정수 변수로 나타내어짐.
- 이진 attributes는 discrete attribute의 한 종류 - Continuous Attribute
- attribute 값으로 실수를 가지고 있음. ex) 온도, 키, 무게 등
- 실제로, 실수는 유한한 디지털 숫자로 나타내어지고 측정되어진다. ex) 디지털 저울
- contiunous attribute는 부동 소수점 변수로 나타내진다. ex) 123.45 * 10^2
<Static of Data>
Measuring the Central Tendency(중심 경향 측정하기), Measuring the Dispersion of Data(데이터의 분산 측정), Covariance and Correlation Analysis(공분산 및 상관관계 분석), 데이터 기본 통계값을 그래프로 나타내는 것을 배운다.
<Basic Statiscal Description of Data> 데이터의 기본적인 통계 설명
- 통계적인 설명이 필요한 이유:데이터를 더 잘 이해하기 위해서(중심 경향성, 분산, 표준편차 등으로)
- Data 분산 특징: Median, max, min, quantiles, outliers
- Numerical dimensions은 정렬된 intervals에 해당한다. (숫자 attribute 가)
- Data dispersion(데이터 분산): 여러가지로 세분화된 분석
- 정렬된 intervals에서 Boxplot 이나 quantile 분석을 한다. - 계산된 측정값에서 Dispersion analysis(분산 분석)
- numerical dimensions로 Folding을 측정함.
- transformed cube에서 Boxplot or quantile analysis
<Central Tendecy 측정하기> : 1. Mean
- Mean (sample vs population)
: n 은 sample size, N은 모집단(population) size

- Weighted arithmetic mean: 가중치 평균 (w=1 이면 그냥 mean에 해당)

- Trimmed mean: 극값(최댓값, 최솟값)을 제외하고 평균 계산.
ex) 올림픽 경기에서 금메달과 꼴등 점수 제외하고 점수 계산 - gymnastics score
<Central Tendecy 측정하기> : 2. Median
- 값이 홀수면 가운데 값이 median, 짝수개면 가운데 있는 2개 값의 평균이 median
- L1: 구간의 최솟값, ∑freq_l: 이전 구간들의 frequency의 합, freq_median: 중간값이 있는 구간의 frequency, width: 값의 범위 (50-21+1=3)
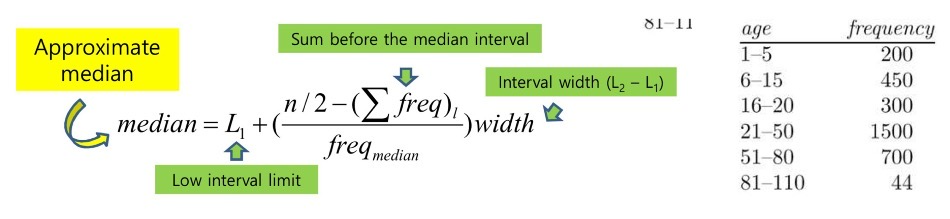
<Central Tendecy 측정하기> : 3. Mode
- Mode: data에서 가장 빈번하게 발생하는 값
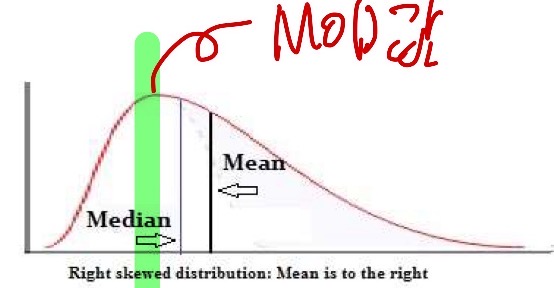
- Unimodal: 1개의 Mode 값
- Empirical formula: mean - mode = 3*(mean-median) - Multi-modal
- Bimodal : mode 값이 2개
- Trimodal: mode 값이 3개
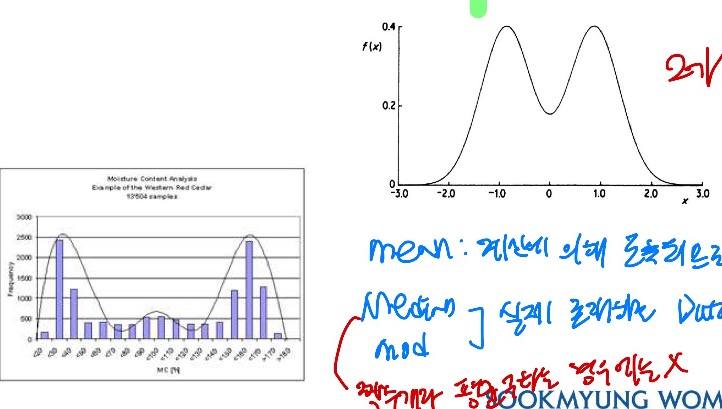
=> mean: 계산에 의해 도출되므로 실제 존재하는 값이 아님. median, mode: 실제 존재하는 Data value (median을 짝수개에서 구하는 경우 빼고)
<Symmetric vs Skewed Data>
- symmetric data, positively skewed data, negatively skewed data의 Median, mean, mode
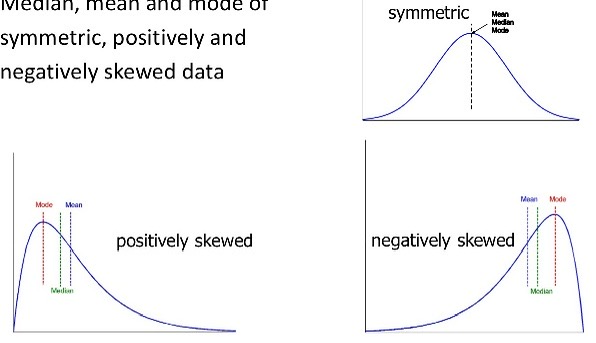
<Normal Distribution Curve(정규 분포 곡선)의 특징>
- symmetric 하다.
- standard로 표준화 한 것은 가운데 central tendency가 0.이다.
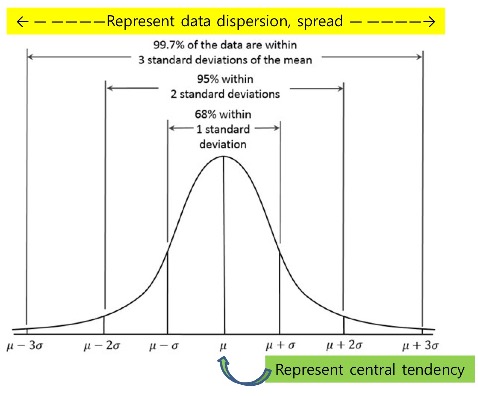
데이터의 분포 측정하기 위해 분산과 표준편차 구할 예정
<Data Distribution(데이터 분포) 측정하기: variance(분산)과 Standard Deviation(표준 편차)>
- 분산과 표준편차 구하기 (s: sample, σ: population)
- 분산 :값에서 평균 뺀 것을 제곱하여 다 더한 뒤, (값의 갯수-1)로 나눔.
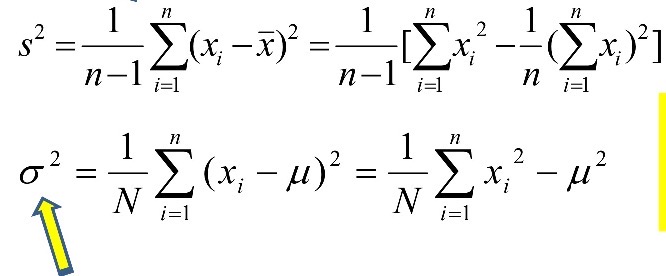
- 표준 편차: 분산에 루트 씌움. √(표준편차)^2
<Correlation Analysis (상관관계 분석) for Categorical Data> 데이터의 상관관계를 분석 ★
- X^2 (chi-square) test 카이 제곱 검정:

- 관측값=기댓값: X^2=0 / 관측값과 기댓값 차이 크면 X^2도 증가
- 기댓값: 두 분포가 독립이라는 것을 기대하는 값
- X^2 값이 클수록 연관성이 있는 것, X^2 값이 작을 수록 독립적이다.
- 가설: 두 분포는 independent(독립)일 것이다.
- Correlation 값(상관관계 값)이 높다고 해서 원인 결과를 말하는 것이 아니다.
- 동시에 증가하거나 동시에 감소하는 연관성이 있는 것이다.
<카이제곱 계산 예시> ★
- 기댓값을 변수로 놓고, 비율 맟춰서 연립방정식 계산하고 기댓값 구함.
관측값 옆 괄호 열고 기댓값 적어놓음
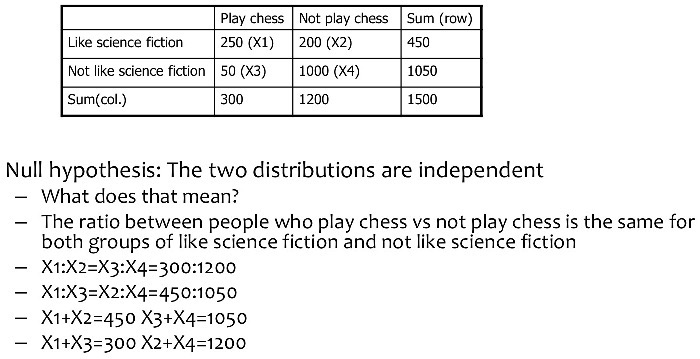
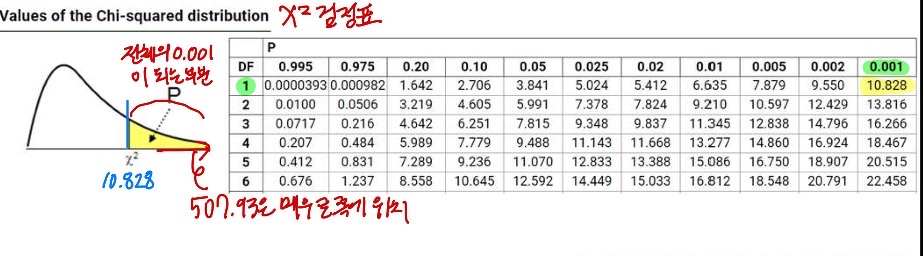
- X^2(카이제곱) 계산(자유도=1 기준으로 계산):
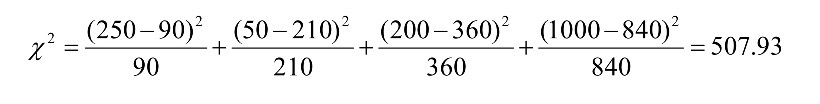
=> 결론: 507.93은 매우 큰 값. 따라서 두 분포 사이에는 연관성이 있다. SF를 좋아하는 것은 체스를 하는 것과 상관이 있다.
- 자유도란?: (Columns 수-1)*(Rows 수-1)
- 카이제곱 분포를 볼 때, 유의 수준과 자유도에 해당하는 값을 기준으로 계산한 값을 평가한다.
- 아래 예시에서는 자유도=1, 0.001 유의수준이므로, 그 기준의 값은 10.828 이다.
- 이보다 크면 카이제곱값이 큰 것 → 두 분포 사이에 연관성이 있다. - X^2(카이제곱) 검정표 보기
<Single data에 대한 Variance(분산) (Numerical Data)> X의 값이 평균, 기댓값에서 얼마나 벗어났는지..
- random 변수 X의 분산: X변수의 값이 X의 평균 or 기댓값에서 얼마나 벗어나는지에 대한 척도를 제공.
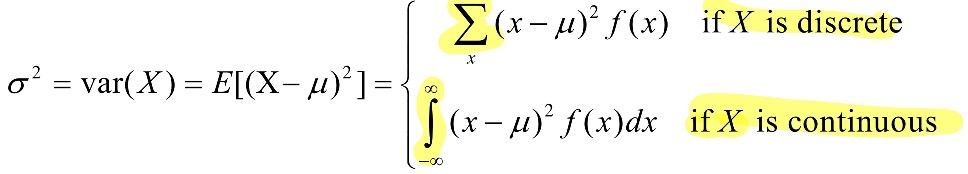
- σ²: X의 분산, σ: X의 표준편차
- μ: 평균, μ=E[X] (X 값에 대한 기댓값)
- σ² = var(X) = E[(X- μ)^2] = E[X ² ] - μ^2 = E[X ²] - [E(x)] ²
- sample 분산
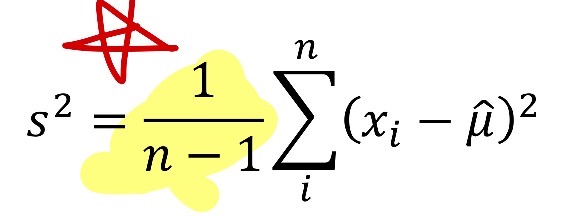
<Two variables(두 변수)에 대한 Covariance(공분산, 동시 변화량)> ★ 두 변수의 동시 변화량을 알 수 있음
- 두 변수 X1, X2에 대한 공분산(Covariance)
- 값에서 평균 뺀 것의 곱셈의 기댓값(평균)
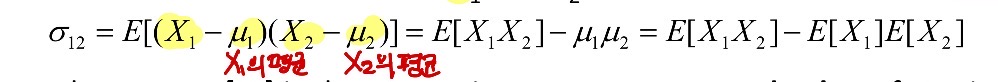
- μ1 = E[X1] : X1의 평균(=기댓값)
- X1과 X2의 Sample 공분산
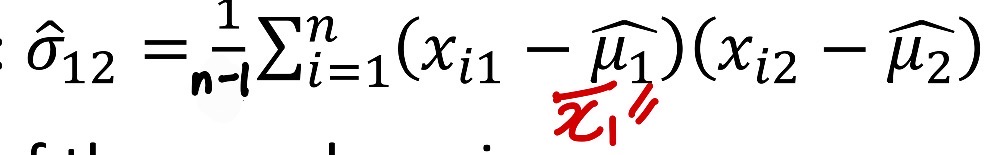
- sample 공분산은 sample 변수에 대한 일반화이다. (일반적인 공분산)
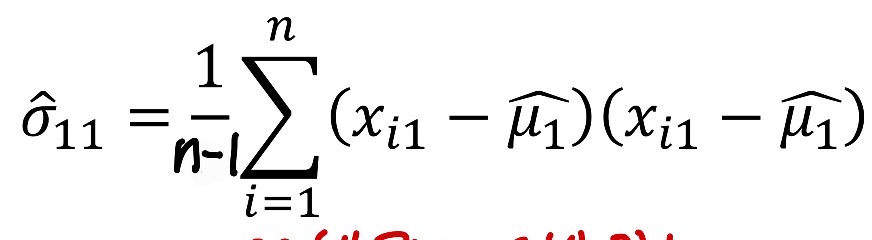
- Positive covariance: σ_12 > 0 (동반 증가, 동반 감소)
- Negative covariance: σ_12 < 0 (한 변수가 증가하면 한 변수가 감소, 한 변수가 감소하면 한 변수 증가)
- Independence(독립)
- X1과 X2가 독립이라면, σ_12 = 0이다. (그 역은 성립하지 않음) - 가정: σ12=0이면 X1과 X2가 독립이다.
- 아래 예시 사진 첨부, 값은 (1, 0), (-1, 1), (-1, -1)가 있음.

- E(X1) = (1-1-1)/3 = -1/3
- E(X2) = (0+1-1)/3 = 0
- E(X1X2) = {(1*0)+(-1*1)+((-1)*(-1))} / 3 = 0
σ12 = E[X1X2] - E[X1]E[X2] = 0 - (-1/3) * 0 = 0: independent를 가리킴 but 실제로 independent 하지 않음
<예시: 공분산(Covariance)의 계산> ★
- X1, X2는 다음과 같은 값을 가지고 있다.: (2, 5), (3, 8), (5, 10), (4, 11), (6, 14)
- 두 변수가 같이 오를지 같이 감소할지 결정하기
- σ_12 구하기 : E[(X1-μ1)(X2-μ2)] = E[X1X2] - μ1μ2 = E[X1X2] - E[X1] E[X2]
- X1, X2의 공분산 σ_12 > 0 이므로 두 변수는 강한 연관성 가지고 있음 전반적으로 동반상승할 것.
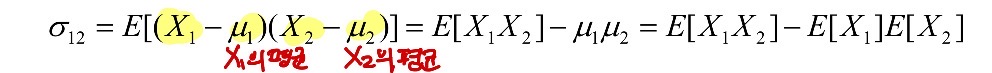
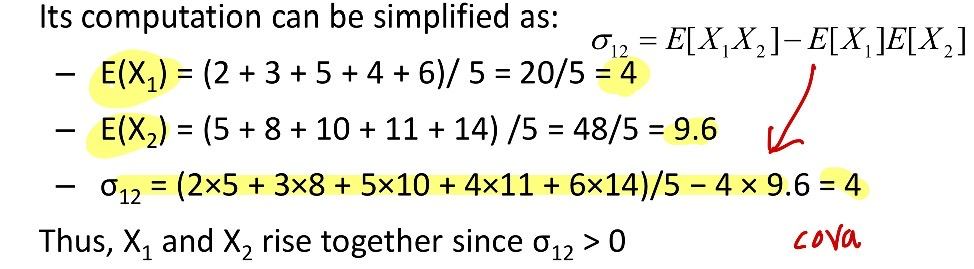
<두 numerical variables(수치 변수) 사이의 Correlation(상관관계)>
- Correlation(상관 관계) =두 변수 X1, X2의 Correlation은 표준 공분산(standard covariance)
- 각 변수의 표준편차로 정규화한 공분산에 의해 얻어진다.
- 정규화된 covariance(공분산) = correlation(상관관계)
- 두 변수 X1, X2에 대한 Sample correlation:
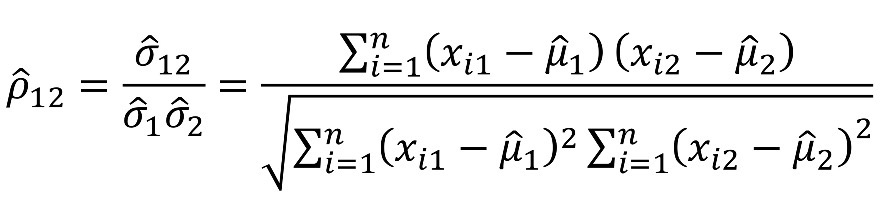
- n: tuple의 개수 / μ1, μ2: X1, X2의 각 평균 / σ1, σ2: X1, X2의 표준 편차
- ρ 12 > 0 : A, B가 positively correlated (A값은 B값에 따라 증가)
- ρ 12 = 0 : independent (독립)
- ρ 12 < 0: negatively correlated (A가 증가할 때 B는 감소)
<Correlation Coefficient (상관 계수)의 Visualizing Change(시각적 변화)>
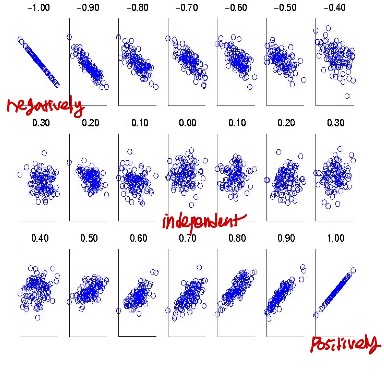
- Correlation coefficient value (상관계수 값) range (범위) : [-1, 1]
- 다음 scatter plots는 상관 계수가 -1 ~ 1로 변화하는 것을 보여줌
<Covariance Matrix 공분산 행렬>
- X1, X2 두 변수에 대한 분산과 공분산 정보 → 2X2 분산 matrix로 요약 가능
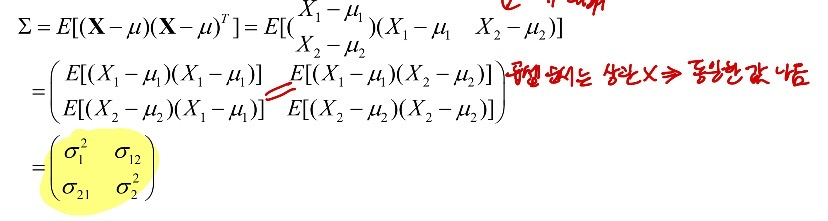

- 변수가 많아서 d차원이 있다면, d*d Covariance Matrix 생성됨
- 대칭 matrix 이다.
<기본 Statistical Description 통계적 설명의 그래픽화>
- Boxplot: 5개의 숫자로 요약해서 그래픽으로 보여줌.
- Histogram: x축은 값, y축은 특정 값.(frequencies)
- Quantile plot: 확률 분포의 분포 형태를 보여줌.
각 값 x_i는 f_i와 쌍을 이루어 데이터의 약 100 f_i%가 ≥ x_i 임을 나타냄. - Quantile-quantile plot(q-q plot): 두 확률 분포의 분포형태를 비교하기 위한 시각적 도구
주로 데이터를 특정 분포(예: 정규분포)와 비교하여, 데이터가 그 분포를 얼마나 잘 따르는지를 확인하는 데 사용됨
데이터 분석에서 정규성 검정 등 다양한 목적으로 활용됩니다. - Scatter plot: 각 값의 쌍은 좌표이며, 이 좌표는 평면에 점으로 표시된다.
<Data의 dispersion(분산) 측정하기: Quartiles & Boxplots>
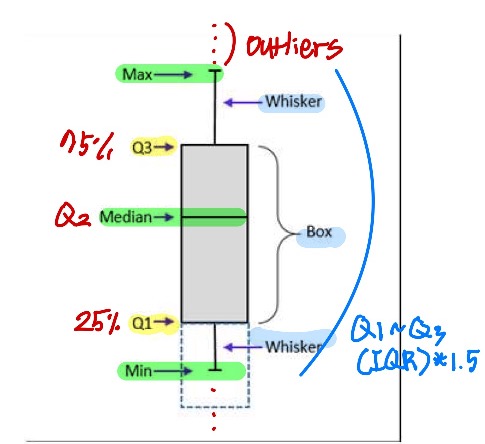
- Quartiles: Q1 (작은 순으로 25%), Q3 (75%)
- Inter-quartile range: IQR = Q3 - Q1
- 5개의 요약 숫자: min, Q1, median, Q3, max
- Boxplot: Box로 나타내지는 data
- Q1, Q3: 박스의 맨 밑(Q1)과 맨 위(Q3), IQR: 박스의 height
- Median (Q2): 박스 안에 선으로 표시되어 있음
- Whiskers: 박스 밖에 있는 선. minimum과 maximum까지 연결해주는 것 - Outliers: outlier threshold(한계점) 밖은 점으로 나타냄.
- Outlier (threshold): 1.5*IQR (Q1~Q3)까지. 각 한계점은 Min과 Max를 나타냄.
<Histogram Analysis>
- Bar chart(막대 차트)와의 차이점
: 연속된 구간을 나타냄. continuous
히스토그램은 변수의 분포를 나타냄, 막대 차트는 변수를 비교하는 데 사용됨
막대 차트에서는 막대를 재정렬 할 수 있음(각각의 값을 나타내므로), 히스토그램에서는 막대를 정렬할 수 없음(연속된 값에 의해 나타내기 때문) - but 각 막대 1개씩은 각 frequency를 나타내므로 discrete함.
<Quantile Plot>
- 데이터의 분포를 보여줌
<Quantile-quantile Plot>
- 두 데이터의 분포를 비교함.
<Scatter plot>
- 각 item에 대한 점을 있는 그대로 보여줌
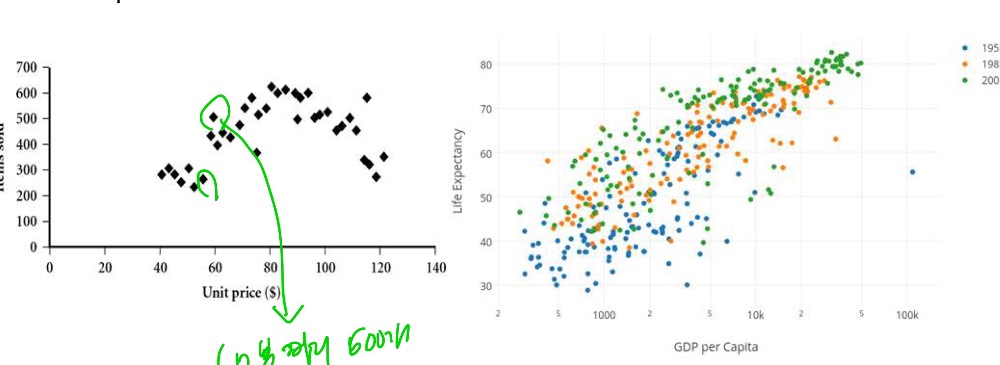
<Similarity, Dissimilarity, Proximity>
- Similarity measure:
두 data objects의 similarity를 측정함: 값이 높을수록 유사하다는 것
[0, 1] 범위에 속하는 것 - 0: 유사성 없음. 1: 완전히 유사함 - Dissimilarity (Distance) measure:
- 두 data object가 얼마나 다른지. similarity와 반대
- 더 낮을 수록 비슷함 (높을 수록 비슷하지 않음)
- 최소 dissimilarity는 0이다. (완전히 유사함)
- (0, 1) 범위를 선호.
<Data 행렬 and Dissimilarity Matrix>
- matrix에 data point를 기록하는데, d(i, j) 로 기록
- 보통 symmetric하다.
- Distance func(거리 함수)는 다양함. (실수, boolean, categorical 변수 등..)
- 가중치를 결합할 수 있다.
<Numeric data (수치 데이터) Standardizing(표준화)>
- Z-score: (변수-μ(mean)) / σ(표준편차)
- μ: 모집단의 mean(평균) - 모집단의 평균과 원시 점수 사이(X)의 거리를 표준 편차 단위로 나타냄 (0~1)
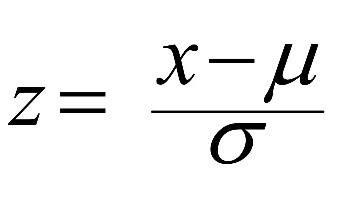
<Numeric Data(수치 데이터)의 거리: Minkowski Distance>
- Minkowski distance: 많이 쓰이는 거리 측정법
- p: 차수 (p=2인 경우 많이 씀)
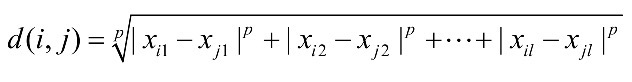
- 특징
- d(i, j) > 0 (if i ≠ j) and d(i, i) = 0 이면 positivity
- d(i, j) = d(j, i) : symmetry
- d(i, j) ≤ d(i, k) + d(k, j) (삼각 부등식) - 위 특징을 만족하는 distance는 metric이다.
- nonmetrc dissimilarities도 있다. .. (?)
<Minkowski Distance의 특별한 case들> ★
1. p=1: (L1 norm) 맨하탄 (city block) distance
- 두 binary vectors의 차의 절댓값을 더함.
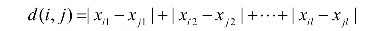
2. p=2: (L2 norm) Euclidean distance
- 두 벡터 차를 제곱하여 모두 더하고 루트 씌움
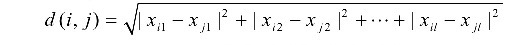
3. p → ∞: (Lmax norm, L ∞ norm) "supremum" distance
- 벡터 간 차의 절댓값 중 최댓값(maximum)
- 제일 큰 값만 남음.
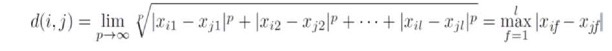
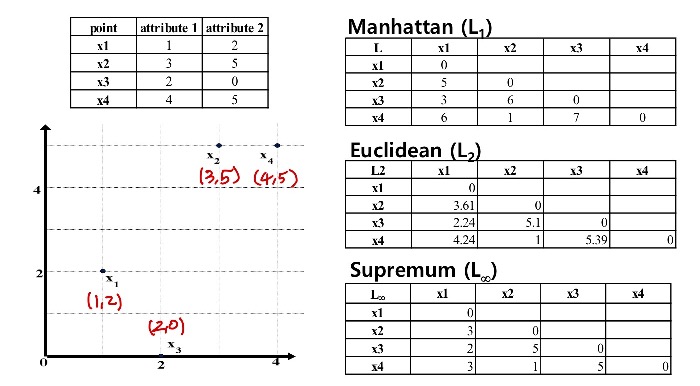
- Minkowski Distance의 특별한 case들: 예시
<Binary attribute에 대한 Proximity Measure(추정치)> ★
- binary data에 대한 인접 테이블
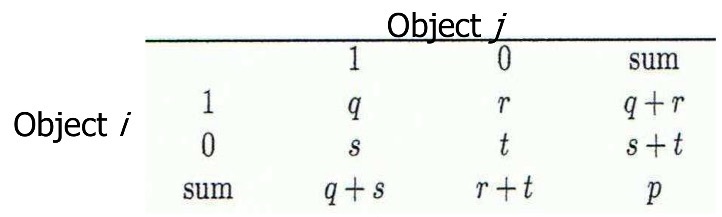
- symmetric binary variables에 대한 거리 측정값
: i ≠ j인 r,s만 분자에 넣음
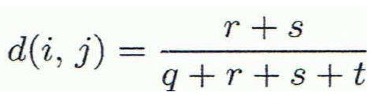
- asymmetric binary variables에 대한 거리 측정값 (둘 다 0인 값인 t는 분모에 넣지 않음)
: i ≠ j인 r,s만 분자에 넣음, 분모에서 t 뺌
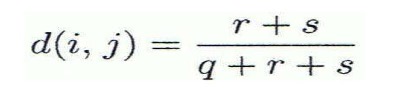
- Jaccard coefficient (Jaccard 상수, asymmetric binary variables의 유사성 척도):
i=j인 것만 분자에 넣음. 분모, 분자에서 i=j=0인 t를 모두 지움.
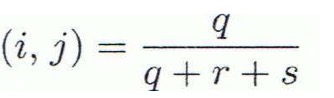
- Jaccard coefficient는 "coherence"와 같다
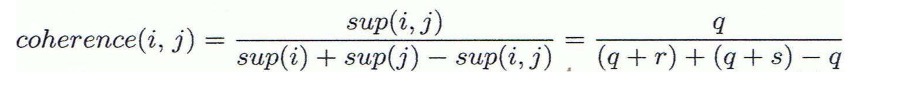
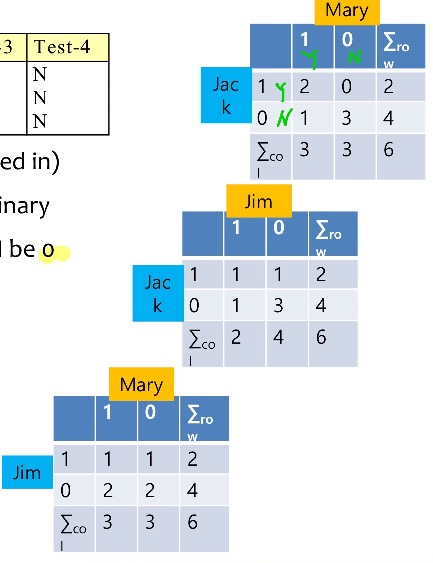
<Asymmetric Binary Variabls 간 Dissimilarity>★
- N=0, Y, P = 1로 놓고 두 사람간 관계를 표로 그림.
- gender attribute는 symmetric이므로 제외, 남은 attributes는 asymmetric binary이다. 이것들 가지고 표 그려라

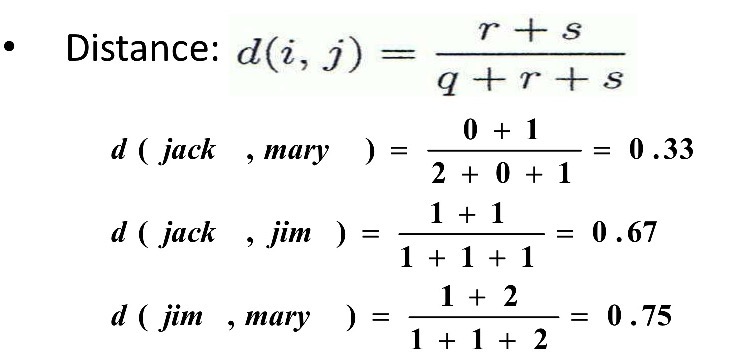
<categorical attributes (nominal)에 대한 근접 측정치>
1. simple matching (m: 매칭의 개수, p: variables의 개수)
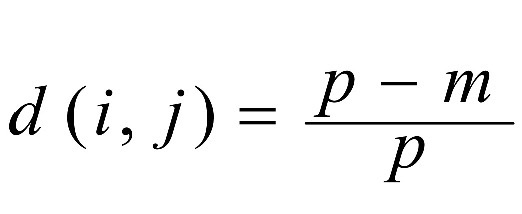
2. binary attributes의 큰 숫자 사용 .A={한, 미, 독}, B={한, 프, 독, 스}일 때 {A∩B} / {A∪B} = 2/5
<두 벡터의 Cosine Similarity> ★
- document는 특정 단어의 frequency를 기록해 단어를 attribute로 삼는다.

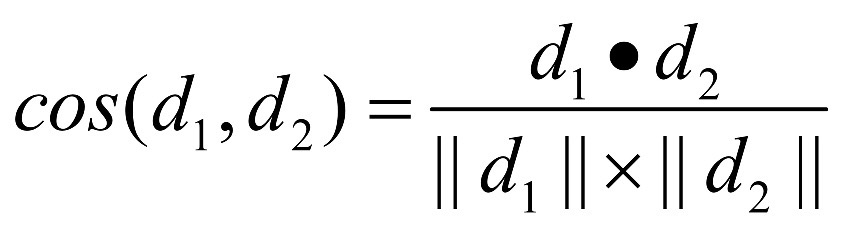
- Cosine measure: d1과 d2 2개의 벡터가 있으면, 아래 식을 이용해 내적함. (두 벡터 사이의 각도로 가까움 similarity 측정)
- 0~1 값을 가짐. 1에 가까울 수록 두 문서가 similar 한 것
- document1과 2사이의 similarity를 측정해라.
- d1 = (5, 0, 3, 0, 2, 0, 0, 2, 0, 0) d2 = (3, 0, 2, 0, 1, 1, 0, 1, 0, 1)

<KL Divergence: 두 확률 분포를 비교>★
- KL Divergence: 동일한 변수 x에 대해 두 확률 분포 간의 차이를 측정함.
- 이를 entrop(예측과 얼마나 비슷한지) 와 cross-entropy(예측과 달라서 놀라운 정도) 개념에 대입해서 유도함.
두 entropy 의 차이로 계산됨
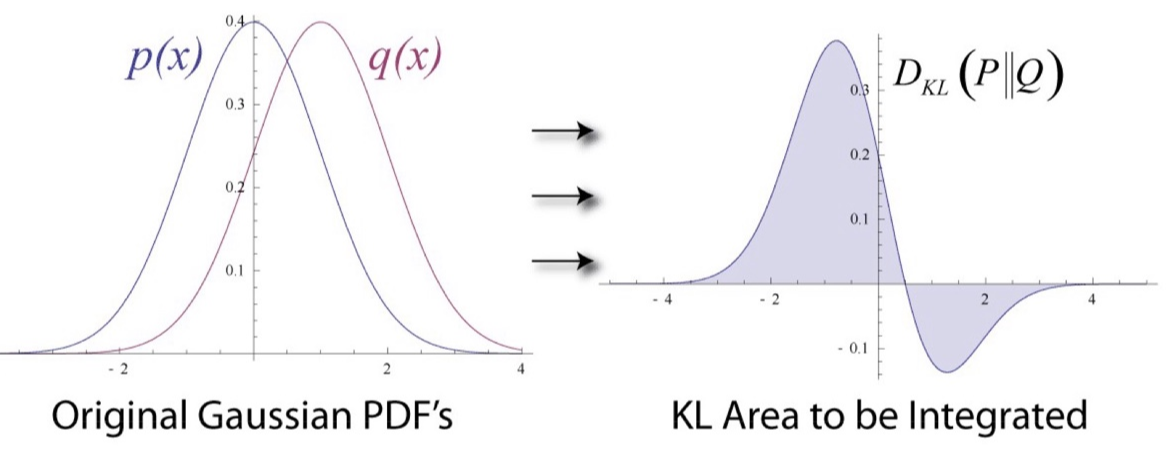
- discrete(이산 분포)일 때는 ∑(시그마), continous(연속형)일때는 ∫ (integral)
- 두 분포, q(실제)와 p (예측)가 있을 때, q와 p의 차이, (p를 이용해 p를 근사화해 p의 손실 정도를 나타냄)
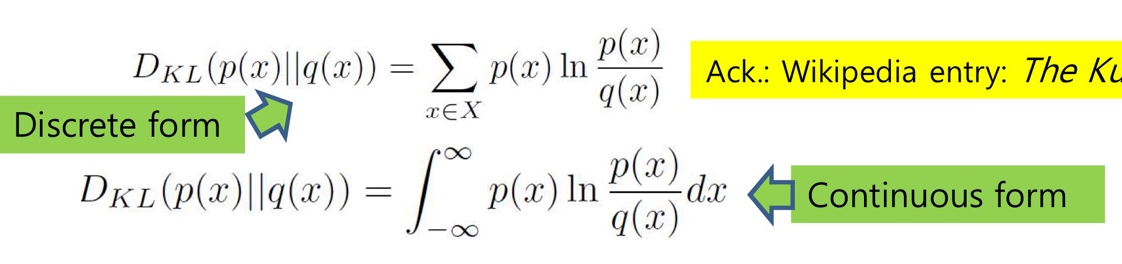
- (정보)엔트로피: -∑plogp
(p: 어떤 값이 나올 확률. 0~1 사이의 값 / log 붙이면 (-)값이 나와서 앞에 (-) 붙여줌) - p: 0~1의 값, 빈번해질 수록(p값 증가) → -plogp의 값 감소 → 빈번한 것에 짧은 bit를 줌 / 빈번하지 않은 것에 긴 bit 줌
- 엔트로피의 예시
: 11010010 처럼 1과 0이 반반인 것이 있다면, 1,0 각각이 나타날 확률 p:1/2
-1/2log(1/2) - (-1/2log(1/2)) = 0 이다.
: 11111111 처럼 1만 있는 것, 1이 나타날 확률 1, 0이 나타날 확률 0
-1log(1) - (-0log(0)) = 0
- 교차 엔트로피(cross entrophy): -∑plogq
- 실제 분포 q를 넣어 비교하므로 식의 결과 값이 커짐. 빈번해질수록 설명의 길이 커짐.(엔트로피와 반대)
- 어떤 것의 차이를 구하고 싶다면. 즉 KL Divergence 구하고 싶다면
-∑plogq - ( -∑plogp )
- 차이 클수록: 두 확률 분포 p, q의 차이가 크다 (p 가 일어날 확률 크다)
- 차이 작을수록: p, q의 차이가 적다 (p가 일어날 확률 적다.)
'공부 > 데이터 마이닝' 카테고리의 다른 글
| [데이터 마이닝] Ch8. Cluster analysis - Density-based/Grid-based (0) | 2024.11.20 |
|---|---|
| [데이터 마이닝] Ch8. Cluster analysis -Hierarchical methods (0) | 2024.11.20 |
| [데이터 마이닝] Pattern Mining: FP-Growth (freq 패턴 마이닝) (0) | 2024.10.10 |
| [데이터 마이닝] Pattern Mining: Pattern Evaluation Methods (1) | 2024.10.02 |
| [데이터 마이닝] Pattern Mining: Methods (Apriori) (1) | 2024.10.01 |