<Ch8. 개요>
- Cluster analysis: 군집 분석
- Partitioning methods: 부분 나누기 방법
- Hierarchical methods: 계층적 방법
- Hierarchical clustering의 기본 개념
- Agglomerative hierarchical clustering (병합 계층적 군집화)
- Divisive hierarchical clustering (분열 일으키는 계층적 군집화)
- BIRCH: scalable hierarchical clustering (확장 가능한 계층적 군집화) using clustering feature(CF) trees (군집 특징 트리를 이용한)
- Probabilisitc hierarchical clustering (확률적인 계층적 군집화)
- Density-based and grid-based methods (밀도 기반, 격자 기반 방법)
- Evaluation of clustering (클러스터링의 평가)
<Hierarchical Clustering의 기본 개념>
- Hierarchical clustering
- clustering hierarchy (군집 계증)을 생성 - dendrogram을 그림
- k(클러스터, 군집의 개수)를 명시할 필요가 없음
- 더 deterministic 함. (예측 가능함)
- iterative refinement (반복적인 정제)가 없음
- Two categories of algorithms (2가지 분류)
1. Agglomerative (병합적): 단일 cluster로 시작 - 계속해서 한 번에 2개의 cluster를 병합 (클러스터의 아래-위 계층 구조를 생성하기 위해)
2. Divisive (분열적): 거대한 macro-cluter로 시작 - 계속해서 2개의 group으로 나눔 (클러스터의 위-아래 계층을 생성하면서)
<Agglomerative vs Divisive Clustering>

<Dendrogram: 어떻게 cluster를 병합할 것인가>
- Dendrogram: data objects의 set을 cluster의 tree로 분해한다. (다중 중첩된 patitioning에 의해)
- data objects의 군집화: 원하는 레벨에서 dendrogrom을 cutting함으로써 얻어짐.
그리고 나서, 각 연결된 구성요소는 cluster을 생성한다. - hierarchical clusterung은 dendrogram을 형성한다. (군집의 계층)

<Agglomerative Clustering Algorithm>
- AGNES (AGglomerative NESting)
- single-link 방법과 dissimilarity matrix(차이점 행렬)을 사용
- 계속해서 가장 작은 dissimilarity를 가진 node를 병합한다.
- 마지막에 모든 node들은 같은 cluster에 속해있음
- Agglomerative clustering은 cluster 간 similarity 척도에 따라 다르다
- Single link (가장 가까운 이웃)
- complete link (지름)
- Average link (그룹 평균)
- Centroid link (centroid similarity 중심 유사도)

<Hierarchical Clustering에서 Single Link vs Complete Link>
- Single link (가장 가까운 이웃)
- 두 cluster 간 similarity: 가장 유사한(가장 가까운 이웃) members 사이의 similarity
- Local similarity 기반: 가까운 지역을 더 강조하고, 전반적인 cluster의 구조는 무시함.
- 비타원형 모양의 objects 그룹을 clustering 할 수 있음.
- noise와 outlier에 민감함.

- Complete link (지름)
- 두 cluster 간 similarity: 가장 유사하지 않은 members 사이의 similarity
- 가장 작은 지름을 가지는 1개의 cluster를 형성하기 위해 두 cluster를 병합
- 비국소적인 행동, compact한 (압축된) 모양의 cluster을 얻음.
- outliers에 민감함.

<Agglomerative Clustering에서 Average vs Centroid Links>
- average link를 가진 Agglomerative clustering
- Average link: 한 cluster 안 하나의 요소과 다른 clusters 요소 사이의 average link
- 두 cluster 내 모든 pairs
- 계산하기 복잡함
- Centroid link를 가진 Agglomerative clustering
- Centroid link: 두 cluster의 centroids 사이의 거리
- Group Averaged(평균화된) Agglomerative Clustering (GAAC)
- 두 cluster Ca와 Cb → Ca∪Cb로 병합
- new centroid: c_a∪b = (N_a*c_a + N_b*c_b) / (Na + Nb)
- Na: cardinality of cluster a (클러스터 a의 요소의 개수) , c_a: centroid of cluster a (클러스터 a의 중심)
- GAAC의 similarity 척도: 두 cluster 거리의 평균
<Ward's Criterion을 이용한 Agglomerative Clustering>
- 결합되지 않은 2개의 cluster Ci, Cj가 병합된다고 가정함
- m_ij: new cluster의 평균
- n_i: cluster 안 요소의 개수
- Ward's criterion (Ward's 표준)
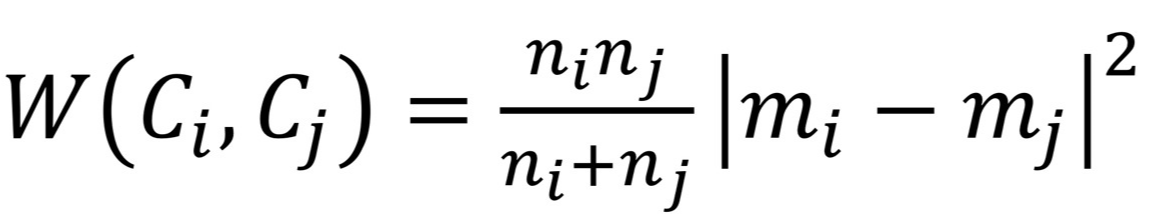
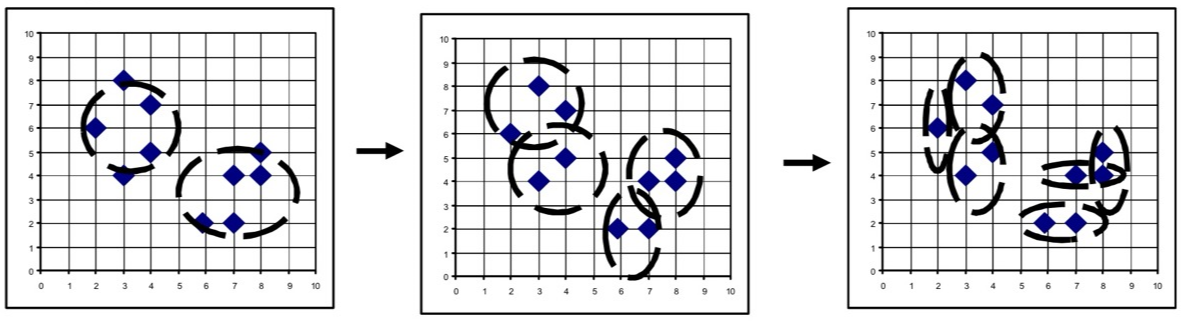
<Divisive Clustering (Top-down 접근)>
- 모든 포인트를 1개의 cluster로 사용한 root에서 시작함
- dendrogram을 만들기 위해 → 재귀적으로 더 높은 level의 cluster로 나눈다.
- global 접근법으로 간주될 수 있음
- agglomerative clustering보다 더 효율적임.
- 어떻게 쪼개야 하는지(쪼갤 cluster를 어떤 어떤 기준으로 선택할 것인지) 정해야 함.
- optimality(최적성) 보장되지 않음, 그저 greedy함.'
<Divisive Clustering의 예시: DIANA> ★
- DIANA: Divisive Analysis
- data set = {a, b, c, d, e} 와 distance matrix가 존재, cluster를 만드는 DIANA를 제공하라.
1. Ci = {a, b, c, d, e}, Cj={ }
2. Ci 내의 각 요소들 사이의 distance 구하고, 평균값 구하기 → 유사도 행렬이 나옴
3. Ci의 각 요소와 Cj 요소 간의 distance의 평균값 구하기
4. (아직 Cj에 아무것도 없다면) Cj 내부에서 차이가 가장 큰 것(Ci 내에서 가장 큰 평균값을 가진 것)을 Cj로 옮기기
5. 2~4를 반복.
6. Ci의 내부 거리의 평균 > Cj의 내부 거리의 평균이면, 가장 먼 거리 (서로 많이 다른 짝)인 cluster 선택. 계속 분리한다는 뜻
8. 모든 cluster가 singleton이 될 때까지 6반복
<Divisive Clustering을 위한 Algorithm 설계>
- 나누기 위한 cluster 선택
- cluster의 제곱 오차 평균을 확인 → 가장 큰 값을 가지는 1개의 cluster 선택
- Splitting criterion (나누기 표준): 어떻게 나눌지 결정
- 나눈 결과로 SSE Criterion에서의 차이를 더 크게 줄이기 위해 Ward's criterion 사용할 수 있음
- 범주형 data에서는 Gini-index가 사용됨
- noise 처리
- 종료 기준을 결정하기 위해 threshold를 사용한다 (너무 작은 cluster은 주로 noises를 포함하기 때문에 생성하지 않음)
<Hierarchical Clustering의 확장>
- agglomerative & divisive hierarchical clustering의 단점
- 재방문을 하지 않음: 이전에 내린 merge/split 결정을 되돌릴 수 없음
- scalability bottleneck: 각 merge/split은 가능한 options들을 조사해야 함
- Time complexity: 적어도 O(n^2) 걸림. (n: 총 object의 개수)
- 몇몇 다른 hierarchical clustering algorithms
- BIRCH: CF-tree를 사용함, sub-cluster의 품질을 점진적으로 조정
- 1단계: K-means 등 clustering을 사용하
- 2단계: Free Clustering을 이용해 data 개수 낮춤
- BIRCH: CF-tree를 사용함, sub-cluster의 품질을 점진적으로 조정
<Clustering Feature Vector>
- 다차원 data object/points의 cluster를 고려함
- cluster의 clustering feature(CF): objects의 clusters에 대한 정보를 요약하는 3-D vector
- cluster의 0번째, 1번째, 2번째 moments를 등록 - Clustering Feature (CF): CF=<n, LS, SS>
- n: data points의 개수
- LS: n points의 linear sum (선형 결합) LS = ∑x_i
- (x좌표의 합, y좌표의 합) - SS: n points의 square sum (제곱 합) SS = ∑(x_i)^2
- (x좌표의 제곱합 + y좌표의 제곱합)
- CF의 장점: cluster을 병합할 때 constant 만에 할 수 있음.
- CF1 + CF2가 O(1) 걸림
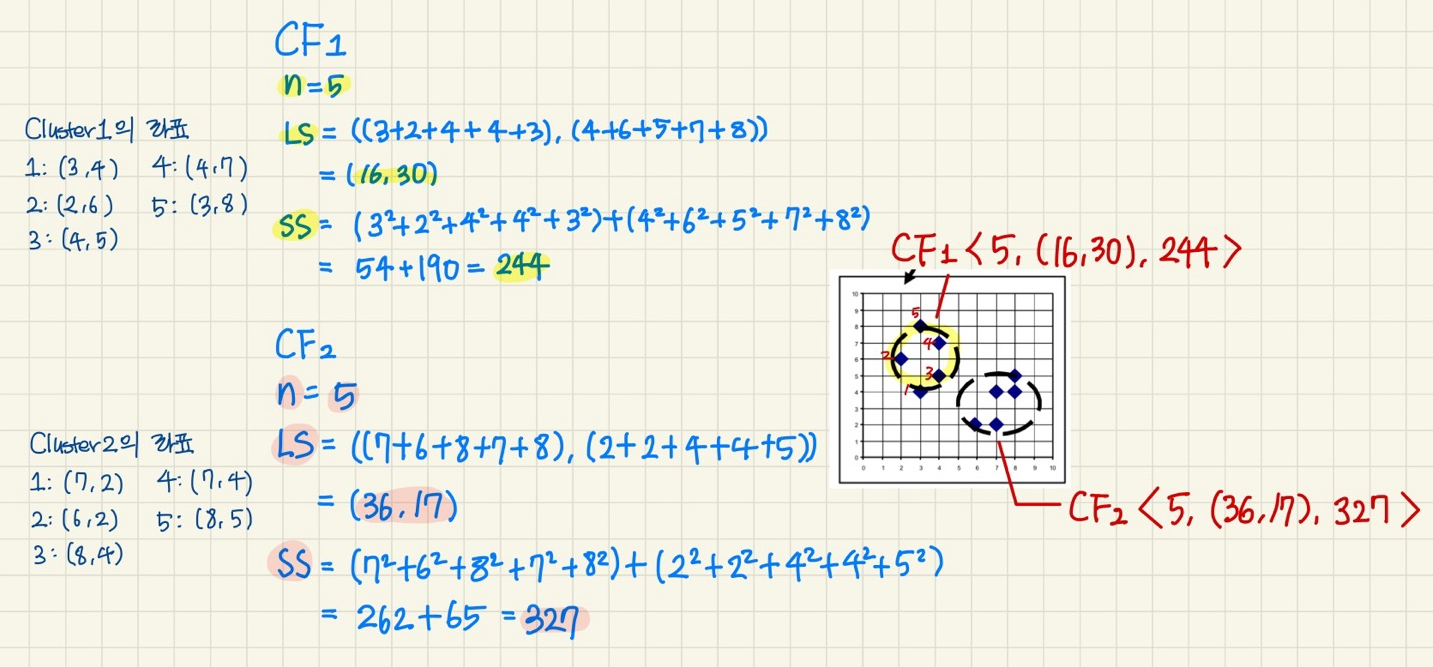
<Clustering Feature: 주어진 cluster에 대한 통계량 요약> ★
- cluster 합성을 위한 중요한 측정을 등록하고 효율적으로 저장공간을 활용함
- Clustering features는 더해진다: Cluster C1과 C2를 병합하기 - CF들의 선형 결합
- CF1 + CF2 = <n1 + n2, LS1 + LS2, SS1 + SS2>
ex) CF1 + CF2 = <5+5, (16, 30)+(36, 17), 244+327> = <10, (52, 47), 571>
<Cluster의 필수 척도: Centroid, Radius, Diameter> : cluster의 중심, 반지름, 지름
- CF를 갖고있는 이유: cluster의 centroid, radius, diameter의 계산을 빠르게 하기 위해
- Centroid : x0
- cluster의 middle
- n: cluster의 point 개수
- xi: cluster의 i번째 point
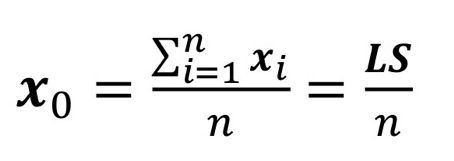
- Radius: R
- centroid와 member objects 사이의 평균 거리
- cluster의 중심 ~ cluster의 어떤 포인트의 평균 거리의 제곱 루트
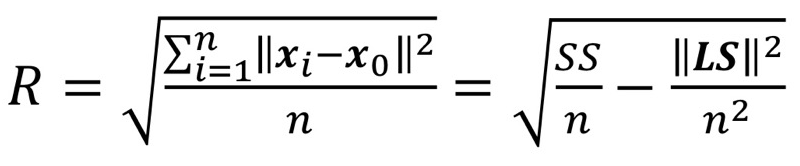
- Diameter: D
- Cluster 내의 쌍별 거리의 평균
- 평균의 제곱 루트: cluster 내에 points의 모든 쌍 사이의 제곱 거리를 의미한다
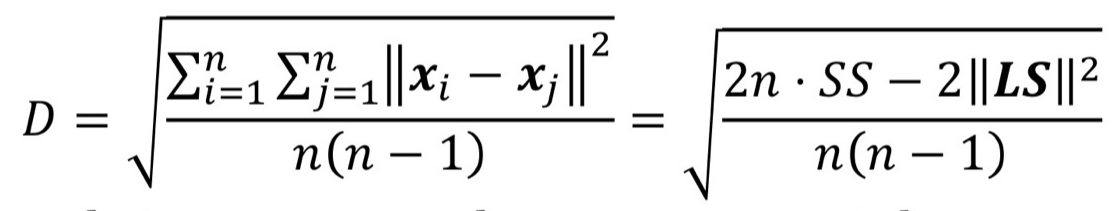
- 예시

<CF Tree: Hierarchical Clustering에 대한 Clustering Features를 저장하는 Height-Balanced Tree>
- 증가하는 new points의 삽입 (B+- tree와 유사)
- B+- tree: tree의 height만 내려가면 원하는 data 찾거나/없다는 사실 알 수 있음 - 각 지점의 삽입에 대해
1. 가장 가까운 leaf entry 찾음
2. leaf entry에 point를 더하고 CF를 업데이트 한다.
3. 만약 entry diameter > max_diameter면: Split leaf거나, parents일 수 있음 - 구체적으로 확인
1. 새로운 point가 들어오면, 가까운 cluster 찾음( 가까움의 기준: 더 가까운 average (LS/n)를 찾으면 됨)
2. L, LS, SS 업데이트
3. 새로운 Diameter D 계산
4. Maximum Diameter과 비교
5. D < Max_diameter면 채우고 끝 (if D > Max_diameter, 초과하면 들어가지 않고 node를 분할함)
이것을 반복하면 값이 채워짐
모든 칸이 다 채워지면, 빈 칸이 없어서 새로운 칸이 필요한 시기가 옴.
- CF tree의 2가지 parameters
1. Branching factor: children의 최대 개수
- 이것이 무작정 크면 좋지 않음. Branching factor 증가 → tree의 height 감소 → node 1개에서 찾는 비용 증가
- log10n < log3n
- B+ tree의 장점: Branching factor의 크기를 고민할 수 있음. 1. balance를 유지하면서 2. Branch factor가 클 수 있다.
- block에 꽉 찰 때까지 factor을 늘림
2. leaf nodes에 저장된 sub-cluster의 Maximum diameter - CF tree: clustering features를 저장하는 height-balanced tree
- height-balanced tree: 새로운 data points 들어가도 root~leaf까지의 거리가 모두 같거나, +-1 차이만 남. tree의 height를 보장 ex) RB tree, AVL tree - non-leaf nodes는 자식들의 CFs의 합을 저장한다.
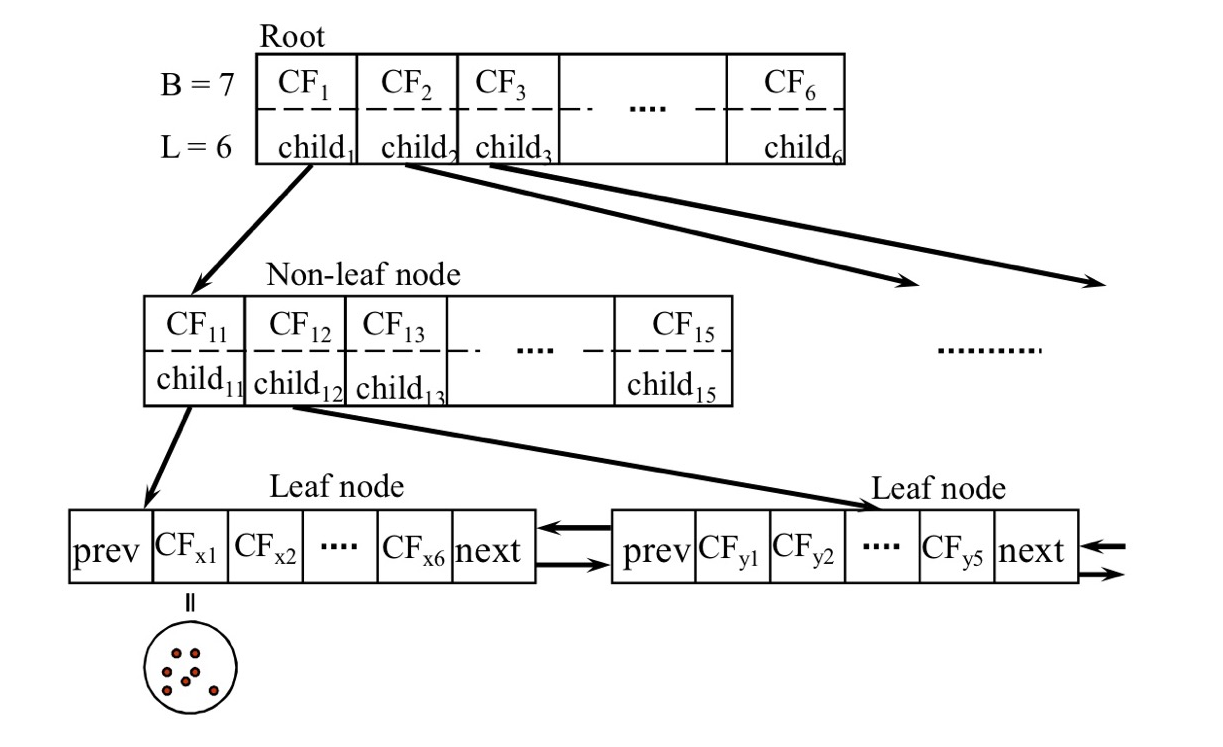
- leaf node에 들어있는 micro cluster의 data의 수 < original(root) data의 수 일 것이다. → max_diameter을 초과하지 않는 범위 내에서 뭉쳐있으므로
- 나머지 clustering은 leaf들만 가지고 진행해라. K-means, Agglomerative 등..
- 아직 cluster라고 부르기에는 작은 cluster지만 original에 비하면 압축되어져 있음
<BIRCH: 확장 가능하고 유동적인 clustering 방법>
- CF Tree 만드는 과정: micro clustering을 하는 과정 ex) 1억개를 만 개로만 줄여보자! 1000개로 나눠보자. 각 cluster마다 10000개가 들어있음
- CF Tree 만드는 시간 (micro clustering) 복잡도: node 거치는 횟수 = O(nlogn)
- BIRCH: 1억개를 가지고 clustering 하지말고, CF Tree의 leaf node인 10000개를 가지고 clustering을 돌려라 (k-means, Agglomerative 등..) → data가 줄어든 상태에서 효율적으로 clustering 할 수 있음.
- CF Tree를 가지고 전체적인 clustering의 속도를 높이자
1. Low-level micro-clustering
- CF-feature과 BIRCH tree 구조를 찾는다.
- data의 고유한 clustering을 보존한다.
- 시간 복잡도(만드는 데 걸리는 시간): O(nlogn)
2. Higher-level macro-clustering
- micro clustering이 끝난 후 leaf node를 가지고 clustering 진행
- 다른 clustering 방법을 사용해 병합에 대해 충분히 유동적이다.
- 시간 복잡도: 위(micro clustering)와 다른 n이다. 위의 것보다 작은 n일 것이다. → 이미 뭉쳐져 있으므로 개수 줄었음
<BIRCH의 장점과 단점>
- 장점
- 클러스터링 결과가 좋은 품질을 보임.
- 시간적 효율성: 크고 방대한 databases들을 선형으로 확장시킬 수 있음(linear scalability)
- 동적 clustering에 효과적이다.(새로운 data가 지속적으로 들어오는 상황에서도 동적으로 클러스터링을 업데이트할 수 있음.)
(CF Tree 생성의 시간 복잡도: O(nlogn) → O(n)이 될 수 있음
- tree에서 node의 절반은 leaf node에 있음. → 초기에 data의 절반은 tree의 height가 낮을 때 삽입됨. O(n)이 될 수도 있다.)
- 단점
- leaf nodes의 size가 고정되어있음. 결과적으로 생성되는 클러스터들이 자연스럽지 않을 수 있음.
(max diameter가 data의 성격에 비해 작거나 큼) → data가 너무 분리되거나 한 node에 다 들어가버릴 수 있음 - cluster은 주어진 radius와 diameter을 기반으로 하기 때문에, 구형(spherical)으로 나타나는 경향이 있음
- leaf nodes의 size가 고정되어있음. 결과적으로 생성되는 클러스터들이 자연스럽지 않을 수 있음.
'공부 > 데이터 마이닝' 카테고리의 다른 글
| [데이터 마이닝] Ch11. Outlier - Basic concept (0) | 2024.12.01 |
|---|---|
| [데이터 마이닝] Ch8. Cluster analysis - Density-based/Grid-based (0) | 2024.11.20 |
| [데이터 마이닝] Data, Measurements and Data Preprocessing (0) | 2024.10.16 |
| [데이터 마이닝] Pattern Mining: FP-Growth (freq 패턴 마이닝) (0) | 2024.10.10 |
| [데이터 마이닝] Pattern Mining: Pattern Evaluation Methods (1) | 2024.10.02 |