1. Basic concept
2. Statiscal approaches
- Parametric methods
- Nonparametric methods
3. Proximity-based approaches
4. Reconstruction-based approaches
5. Clustering and Classification based approaches
6. Mining contextual and collective outliers
7. Outlier detection in high-dimensional data
<Statical Methods의 General idea>
- 주어진 data set의 분포를 잘 설명하는 생성 모델을 학습하고, 그 모델에서 낮은 확률 영역(low-probability regions)에 속하는 objects를 outliers로 식별한다.
- parametric method: normal data objects가 유한 개의 parameter를 가진 특정 parametric 분포에 의해 생성된다고 가정함.
- parametric 분포의 확률 밀도 함수를 사용해 object가 해당 분포에 얼마나 잘 맞는지 평가.
- 확률 밀도 함수의 값이 작을 수록, 객체 x는 분포에 잘 맞지 않음 → outlier일 가능성이 높음. - non-parametric method: 특정 분포를 가정하지 않고, data 자체의 패턴이나 분포를 학습해 outlier를 감지함.
- 특정 분포를 가정하지 않고, data 자체의 패턴이나 분포를 학습하여 이상치를 감지
- parametric method: normal data objects가 유한 개의 parameter를 가진 특정 parametric 분포에 의해 생성된다고 가정함.
<Parametric method: 1. 정규 분포에 의한 단변량 이상치 탐지 (detection of univariate outlier)> 단일 변수만 고려
- 주어진 data가 정규 분포(가우시안 분포)를 따른다고 가정 (data가 평균 μ 과 표준 편차 σ 를 가진 분포에서 생성됨)
- 방법: 입력 데이터로부터 정규 분포의 파라미터(평균 μ 과 표준 편차 σ)를 학습 → 확률 밀도 함수를 사용해 각 데이터가 정규 분포에 속할 확률을 계산 → 낮은 확률(low probability)에 위치한 points를 outlier로 식별함.
- 확률이 0.15% 미만인 데이터는 outlier로 간주 - e.g.) 과거 10년 간 7월 평균 온도 [24.0, 28.9, 28.9, 29.0, 29.1, 29.2, 29.2]
1. 정규 분포의 두 파라미터 ( 평균 μ, 표준 편차 σ) 측정

2. 파라미터를 이용해 확률 밀도 함수 계산

- L(24|(28.61, 2.29)) < 0.15% 이므로, 24.0℃ 는 outlier 이다.
<Parametric method: 2. Boxplot Visualization>
- The interquantile range(IQR, 분위간 범위): Q3 - Q1
- Outlier: Q3에서 1.5*IQR 보다 큰 구간에 해당하는 objects
Q1에서 1.5*IQR 보다 작은 구간에 해당하는 objects

<Parametric method: 3. Grubb's Test>
- data set에 각 object x가 있다고 하자. μ: 입력 데이터의 평균, σ: 입력 데이터의 표준 편차
- z-score은 아래와 같다.

- object x가 outlier가 되는 기준


- 기준에 들어있는 위 식은 유의 수준(α/2n, α는 사용자가 임의로 결정)에서 t-분포가 취하는 값.
- t 값: t-분포 표에서 구하기.
<Detection of Multivariate Outliers(다변량 이상치 탐지): Mahalanobis distance > 변수 여러개일 때, n차원
- Multivariate Outlier detection(다변량 이상치 탐지)를 Univariate Outlier detection(단변량 이상치 탐지)문제로 변환
- Multivariate outlier detection은 Mahalanobis distance를 사용
- o: outlier인지 확인하고 싶은 data object, o': 평균 object
- S: covariance(공분산) matrix (e.g.: 3차원이면 3*3 covariance matrix)

- MDist(o,o'): object o와 평균 o' 사이의 마할라노비스 거리

- object o: 1xd 전치 행렬, * dxd 행렬 * d*1 행렬 = 1x1 행렬 나옴.
- 그래서 Mdist(o, o')를 계산하면 1차원으로 바뀜.
- 1차원에 normal distribution, Boxplot, Grubb's test 등을 적용.
<Detection of Multivariate Outliers: X^2-statistic (카이 제곱)>
- X^2-statistic: 테이블 형태로 해석하여 카이제곱검정 실시

- o_i: i번째 dimension에 있는 특정 object의 값(outlier를 탐지할 object)
- E_i: i번째 dimesion의 모든 object의 평균
- X^2-statistic이 커서 유의 수준의 임계 값을 넘으면, object는 oulier이다.

- 실제 세계의 데이터는 하나의 분포로부터 생성된 data만 있을 가능성 적음. 여러 원인에 의해 생성된 data가 mix되어있을 것
e.g.) 실제 세계에서는 가지고 있는 씨앗이 쌀 뿐만 아니라 잡곡인 경우가 많음. 하나의 normal distribution으로 나타내기 힘듦. → outlier 탐지 어려움 - 하나의 분포가 아닌, 여러 분포로 나온 data가 섞여있을 것 → 여러 분포 모델로부터 가중합을 구해야 함(어떤 분포를 따를 확률은 0.9, 어떤 분포를 따를 확률은 0.1)
- outlier 탐지에 여러 분포 모델을 사용해야 함
- 가지고 있는 data의 확률 분포 밀도 함수를 어떻게 표준형으로 정의할 건가? (아래에 답 나옴)
<Non-parametric Method: Histogrom>
- outlier가 존재하지 않는 train data(input)로 히스토그램 그림.
- 가지고 있는 sample에 따라 histogram의 모양 달라짐
- 판정하고 싶은 data가 어느 구간에 들어가는지 보고 outlier 판정
- 매우 확률이 높은 쪽에 들어가면 outlier일 확률 적음, 확률이 낮은 쪽에 들어가면 outlier일 확률 높음.
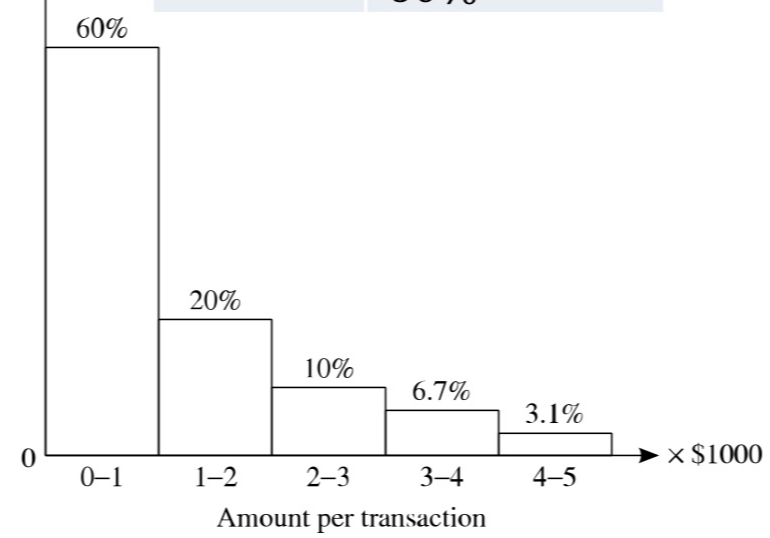
- 히스토그램 해석: 5 이상의 구간에 들어가는 object는 outlier이다.
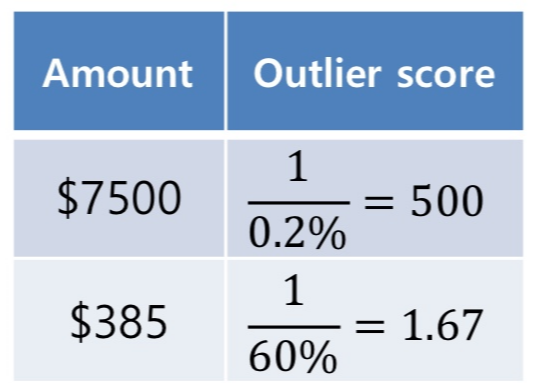
- outlier score 계산 (threshold 주어질 것)
- $7500이 outlier 일까? : $7500이 해당하는 구간(5 이상)의 확률을 역수로 취함. 1/0.2% = 500
- $385가 outlier일까?: $385가 해당하는 구간(0-1)의 확률을 역수로 취함. 1/60% = 1.67 - threshold score보다 높은 점수를 가진 값은 outlier. (threshold=100이면, $7500은 outlier)
<Non-parametric Method: Kernel Density Estimation>
- Kernel funcion K(): 조건 1. 음수부터 양수까지 값의 면적이 1이 되어야 하고, 조건 2. 그 면적이 대칭이어야 한다.
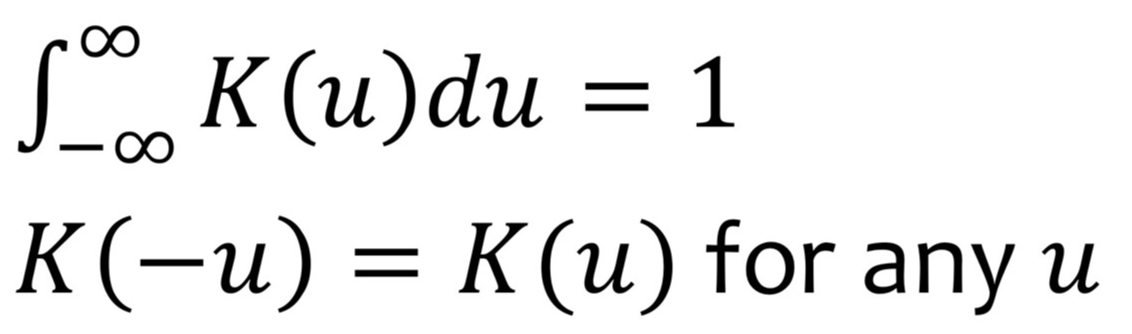
- 다양한 function 쓸 수 있지만, 대표적인 것은 평균이 0이고 분산이 1인 standard Gaussian function이 있다.
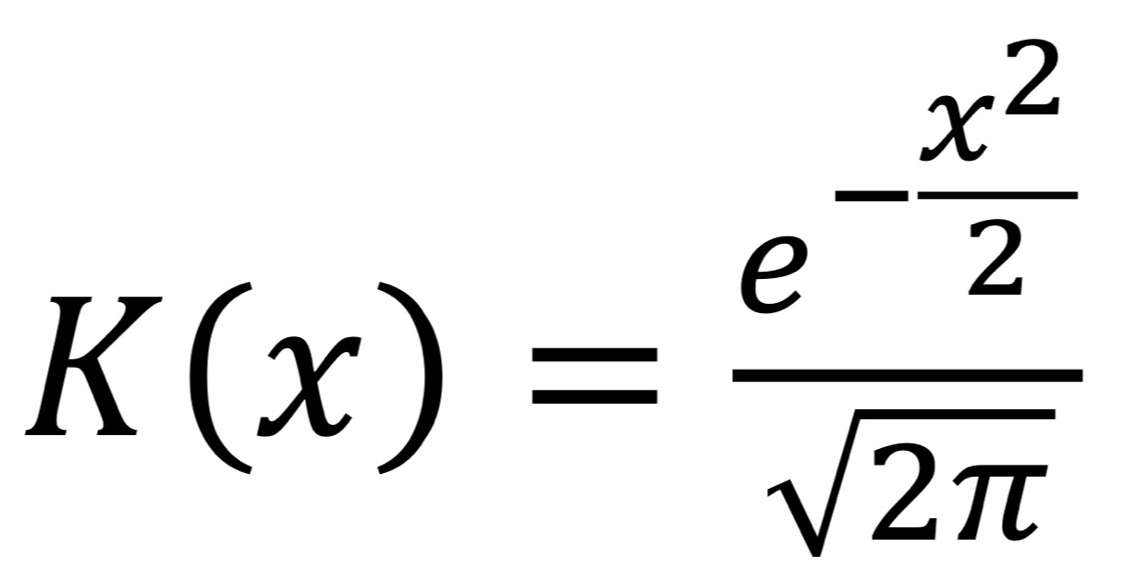
- K() 정했으면, 확률 밀도의 kernel density approximation: Kernel 함수를 사용해 데이터의 확률 밀도 함수를 추정
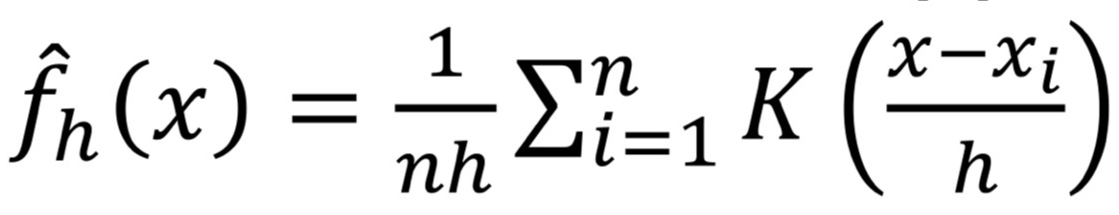
- x: outlier 판단할 data object, x1, x2, ..., xn: train data
- K(): Kernel function, h: smoothing parameter로 쓰는 bandwidth
- n: 합쳐져서 커진 값을 낮춰주는 역할
- h: bandwieth. 데이터를 smooothing하는 parameter
normal distribution 더할 값의 범위를 낮춰줌. 모인 정도를 조절하고 싶을 때 사용
h가 작을 수록 가까이 있는 값의 영향을 받음(추정이 세밀함) / h가 커질수록 멀리 있는 값의 영향도 받음.(추정이 부드러움)
여러 kernel function에 대한 중첩도를 나타내는 parameter
- K() 내부 설명: x-xi인 값을 K()에 넣어서 i: 1~n까지 돌린 것을 합친 값을 K()에 넣어줌
- 정리: 각각의 분포를 더해서 → n으로 나눠 평균값을 줄이고 → 그때의 density값을 읽어서 outlier 판정,
h로 나누면 h가 클수록 멀리 떨어져 있던 애들도 가깝게 모음. 멀리 있는 것에서부터 영향 받음. h가 작아지면 가까운 애들에만 영향을 받음 (멀리있는 것의 영향력 작아짐). - 여러가지의 분포가 섞인 상황을 해결할 수 있는 방법
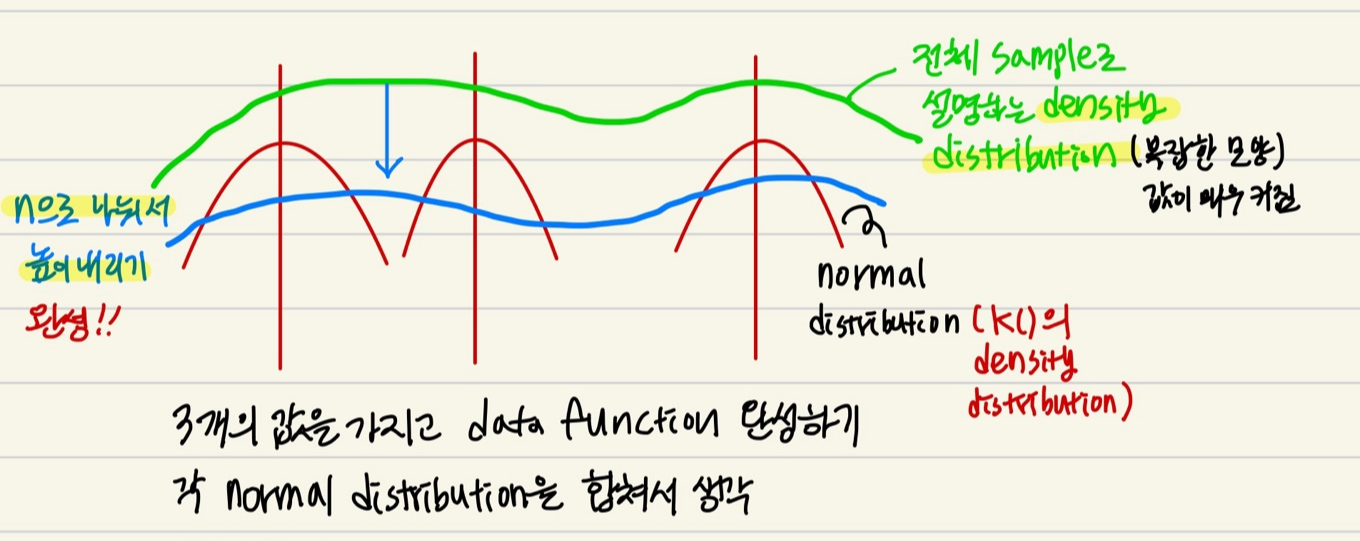
- data point에 해당하는 하늘색 density distribution의 값을 구함
- 값까지 낮춘 하늘색 density distribution의 값 큼 → outlier일 확률 낮음
- 값까지 낮춘 하늘색 density distribution의 값 작음 → outlier일 확률 높음
<Statical Method의 장단점>
- 장점: outlier detection이 수학적, 통계적으로 정립이 되어있다.
- 단점: high-dimesional data(고차원 데이터)에서 outlier detection이 어려움
<Proximity-Based Approaches> = Algorithms-Based
- 분포 모델에 기반한다기 보다는 특정 target을 정하고 target을 찾기 위한 알고리즘을 찾는 방법 (실세계에 존재하는 다양한 data에 적용하기에 좋음)
- statiscal은 수학적 정의를 활용한 outlier를 사용, Proximity는 outlier의 정의가 논문의 저자에 따라 다름. (어느정도는 상식에 부합)
- 직관: 다른 objects로부터 멀리 떨어져 있는 objects는 outlier로 간주될 수 있다.
- Proximity-based outlier detection의 2가지 종류
1. Distance-based methods: 절대적인 거리 고려해서 neighborhood 설정 → objects 주변의 neighborhood가 충분히 많지 않을 경우, object를 outlier로 간주.
2. Density-based methods: objects 주변의 밀도 < 주변 neighborhood의 밀도 (상대적으로 낮을 경우) 이면, 해당 objects를 outlier로 간주. local outlier를 찾는 방식에 가까움.
- (local outlier: 전체 data 분포의 일부분에서 outlier가 될 수 있는 경우 / context outlier: context에 의해 subset이 만들어지고, 각 subset 내에서의 outlier를 정의하는 것)
- (collective outlier: 기존 outlier들은 sparse함. 혼자만 다르다. but collective는 뭉쳐서 튀어서 outlier로 취급)
<Distance-Based Outlier Detections> global outlier 찾기
- object o: outlier인지 판단하고 싶은 data
- parameter: r (distance threshol, r ≥ 0), π(fraction threshold, 0 ≤ π ≤ 1)
- object o가 DB(r, π)-outlier일 경우,
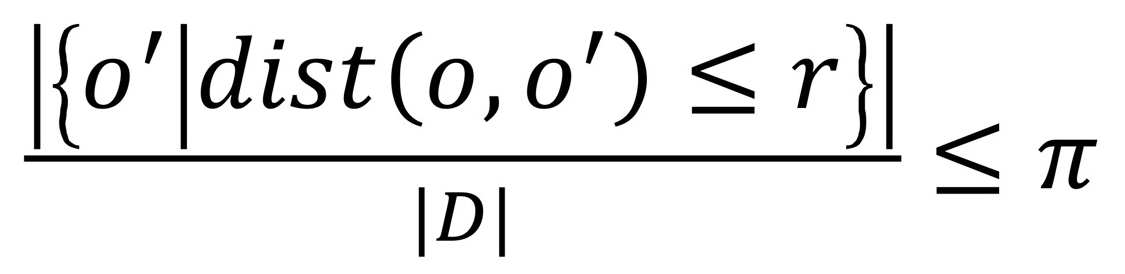
- o를 기준으로 r 안에 있는 o'의 비율 ≤ π 이면, o는 outlier이다.

<Density-Based Outlier Detection>
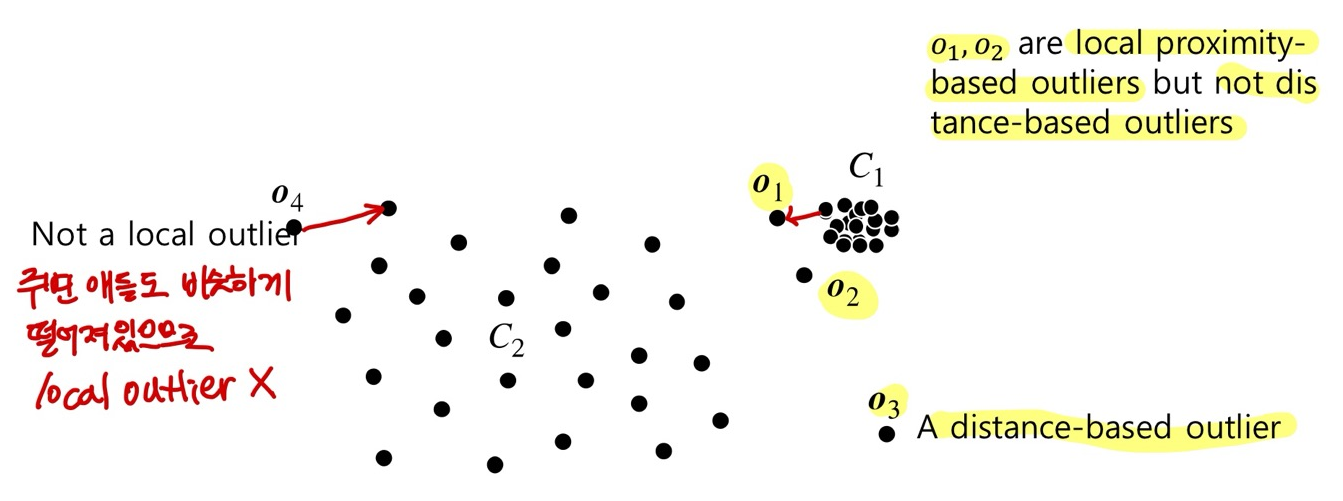
- Local proximity-based outliers (local outlier를 찾겠다): 지역적으로 비슷함의 기준이 다르게 판정된다.
- 한계: 어떻게 object의 상대적인 density를 측정할까? → 내 주변 다른 data point가 나에 비해 얼마나 떨어져 있는지, 상대적인 거리 중요
<k-Distance> 중요★
- dist_k(o): 어떤 data object o로부터 k번째 가장 가까운 이웃까지의 거리
- N_k(o): k-nearest neughbor, dist_k(o) 이하의 거리를 가진 모든 객체 o'(data points)의 집합.
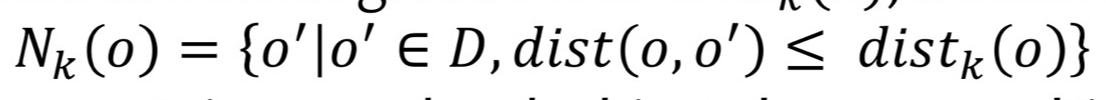
- N_k(o) ≥ k개: 가능. k가 공동이 있을 수 있다. k번째와 동일한 거리를 가진 object가 여러 개일 수 있음.
N_k(o) < k: 불가능. data의 개수가 k보다 작으면 k번째를 논할 수 없음. - 순서를 잘 보고 k를 따져야 함. 중요!
<Reachability Distance와 Local Outlier Factor> local outlier 구하기 ★
Reachability Distance의 정의
- dist(o, o') > dist_k(o)라면, o'에서 o까지 reachability distance: dist(o, o')
dist(o, o') < dist_k(o)라면, o'에서 o까지 reachability distance: dist_k(o)
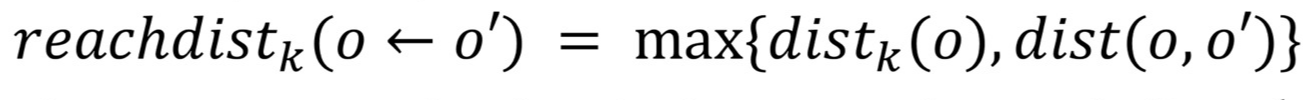
o'가 나(o)와 너무 가까이 있다면(N_k(o) 중 하나라면), dist_k(o)을 쓸 것이다.
o'가 나(o)와 너무 멀리 있다면(N_k(o)가 아니라면), dist(o, o')를 쓸 것이다.
- reachdist_k( o ← o' ) ≠ reachdist_k( o'← o ):
Reachability Distance는 symmetry가 아니다. 방향성이 존재함.
(상대가 나의 nearest neighbor라고 해서 나는 상대의 nearest neighbor이 될 수 없음.) - Local reachability density: object o의 density (o에 대해서로 정의)
뒤집으면 평균 거리(density 만들기 위해 역수로 만듦)
reachdist_k 클수록 deinsity 작음 / reachdist_k 작을수록 density 큼.
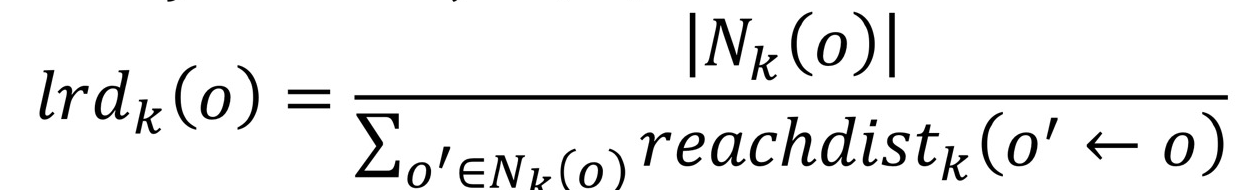
- object o의 Local outlier factor: 내 neighbor의 각각의 density와 나의 density 비교. Neoghbor과 density 얼마나 비슷한가.
- lrd_k(o) 값이 1: 주변 neighbor와 거리가 비슷. density가 비슷함.
lrd_k(o) 값 < 1: 주변 neighbor과 거리가 다름. density 다름. outlier일 가능성 증가 (local outlier) - 절대적인 density가 중요한 것이 아니라, 주변과 density가 얼마나 다른지 상대적인 density 따짐
- density 기반으로 local outlier 찾는 것