1. Basic concept - outlier은 normal한 패턴을 따르지 않는 것
2. Statiscal approaches: 통계적 기법으로 outlier 찾기(box plot, normal distribution, t-distribution, distance-based, realistic k로 local outlier)
3. Proximity-based approaches
4. Reconstruction-based approaches - normal한 방법을 대표하는 모델 (succint represention)으로 복원시켰을 때, normal한 것은 모델을 따르고, outlier은 모델을 따르지 않음.
5. Clustering and Classification based approaches - 클러스터링으로 outlier라고 define 되는 것은 outlier다, Cluster가 너무 작으면 outlier / outlier로 labeling된 것, normal이라고 labeling된 것 중 outlier로 labeling된 것을 학습해서 normal 점수가 높으면 normal, outlier 점수가 높으면 outlier
6. Mining contextual and collective outliers
- Transforming Contextual Outlier Detection to Conventional Outlier: context를 정의하는 attribute가 있음. 이거대로 subset을 만들어 각 subset 안에서의 conditional 조건을 가지고 판단했을 때, 확률이 너무 낮으면 outlier / data가 모여있는 결과 (data의 특성대로 모인 결과)가 특이하면 outlier로 봄.
- Modeling Normal Behavior with Respect to Contexts
- Mining Collective Outliers
7. Outlier detection in high-dimensional data
<Identifying Context> Context 식별하기
- Contextual attributes: 나이 그룹(25 이하, 25-45, 45-65, 65 이상)
- Behavioral attributes: 연간 거래 횟수 (고객이 1년 동안 거래한 총 횟수), 연간 총 거래 금액
- V: Behavioral, U: Contextual
- 어떤 data object가 자신의 context에서 자신의 bevior을 가질 확률이 얼마나 되는지
- 확률 높아면 outlier 아님, 확률 낮다면 가끔 일어나는 일이므로 outlier
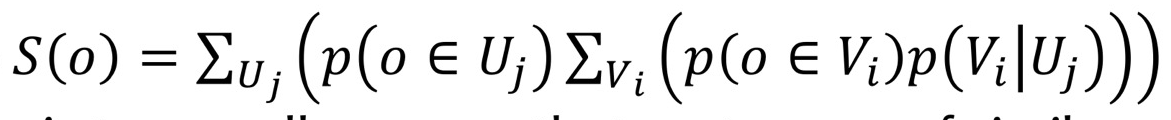
- 앞에 붙은 식
- object가 여러 context에 속할 수 있음, 여러 behaivor에 속할 수 있음. 이것을 다 더하겠다는 뜻
- 내가 속한 behavior가 1개이고, 내가 택할 수 있는 context가 1개만 있다면 - context를 너무 세밀하게 쪼개면, 세밀하게 쪼갠 context에 속하는 case(data object)가 매우 작음
outlier 판정에 대한 사례가 너무 없으니 context를 넓히기 위해 (주변 것과 합침, generalize) 좋음.
→ normal과 outlier에 대한 판정이 쉬워짐. - e.g.) ~한 아파트까지 따지면 case가 너무 없음. 구,동 까지 넓혀서 보자(generalize)
<Collective Outliers>
- 개별적으로 보면 모르지만, 뭉쳐있으면 집합적으로 outlier로 판정할 수 있음.
- 어떻게 뭉쳐야 할까?
- temporal data (시계열 데이터): 시간 관점에서 집합을 형성해야 함.
e.g.) 시간 단위로 뭉쳤을 때, 평균 초당 100번 access를 가지고 있던 게 갑자기 초당 100000번 access를 함.
→ 특이 access가 보이므로 outlier - spatial data: 지역적으로 집합 형성
e.g.)갑자기 여러 지역에 분포되어있던 로또 당첨자가, 특정 지역에서 로또 당첨차가 많이 발생하면, 지역적으로 묶어봤을 때 outlier임을 판정 - graph data: subgraph를 봐야 함.
e.g) graph 형태의 data에서 subgraph를 뭉쳐진 것으로 봄. → subgraph 빈도수 freq(S)가 높으면 outlier, 낮으면 outlier
- temporal data (시계열 데이터): 시간 관점에서 집합을 형성해야 함.
- collective oulier는 이런 구조들(집합들)이 명시적으로 정의되어있지 않기 떄문에, oulier detection 과정에서 구조를 발견해야 함.
<Graph data의 Collective Outlier Detection>
- Graph data에 나타나는 각 subgraph를 구조적 단위로 간주함.
- subgraph: data에 똑같은 subgraph가 나타남. 이것이 몇 번 등장하는가? 를 셈
- |S|: Subgraph S의 정점 수
- freq(S): Graph data에서 S와 모양이 같은 서로 다른 subgraph 수
- subgraph가 너무 빈번하거나(freq(S)가 매우 큼), 너무 적으면 (freq(S)가 매우 작음) → outlier일 가능성 높음

- 왜 자주 등장한 경우가 outlier가 되는가? : outlier는 normal한 패턴을 따르지 않는 것. 빈번한 것이 normal한 패턴을 따르지 않으면 그것도 outlier
<High Dimensional Data에서 Outlier Detection>
- 역시 어렵다. 까다롭다.
- Data sparsity: dimension이 많으면 object 간의 거리가 점점 더 noise에 지배된다. 일정하게 sparse하게 됨.
- Dimesion이 많아지면 다른 data와 얼마나 떨어져 있는지에 대한 절대적인 크기가 비슷해짐. (근접성 측정하기 어려워짐)
<전통적인 Outlier Detexction을 확장하는 방법: rank>
- data 간 거리(절대적인 크기)가 비슷해지더라도, 순서가 나오므로 비교해봐야 함.
- 부분공간을 구성해서 그 안에서 outlier을 탐지.
- HillOut 알고리즘:
각 object에서부터 k-nearest 안 1~k번째 까지의 값을 모두 더해서 sort하면 더한 값의 순서가 나온다. - outlier면 K-nearest까지 더한 값이 클 것이다.
- 얼마나 큰지는 알 필요 없음(너무 커요).
rank (l) 정해서 가장 큰 것 l개까지만 보고 값 판단.

- 객체 o의 최근접 이웃: nn1(o), nn2(o), ..., nnk(o)
- k: 조정 가능한 매개 변수
<Subspaces 에서 Outlier 찾기>
- 모든 dimesion 말고, 일부 dimension만 사용하겠음.
- Subspace: 일부 dimension
- Subspace를 가지고 outlier 판단하는 것이 의미가 있음.
- e.g.) Alice를 구성하는 것에는 나이, 소득, 좋아하는 음식, 좋아하는 계절... 등 이 있음. 이 사람이 outlier인지 판단하려면?
모든 특성을 가지고 판단하지 못 함. 특성 중 2가지 특성인 평균 구매액수, 카드 사용 빈도를 이용해 '카드를 얼마나 쓰는 사람인지?' 판단 → 카드를 잘 안 긁는데, 한 번에 큰 금액을 씀. → 2가지 dimension에서 outlier이다. - 일부 dimension을 어떻게 골라내는가?
<Grid-Based Subspace Outlier Detection Method>
- 각 dimension을 histogram으로 만들어보자.
- equial-depth 방법: 높이를 같게, 구간의 폭을 다르게 (frequency를 통일해야 하므로 data 적은 부분은 구간 넓게, data 많은 부분은 구간 좁게)
- 각 차원 당 구간의 개수 =∮개, 한 구간에 들어오는 data의 비율 f = 1/∮
<Grid-Based Subspace의 Sparsity 측정>
- data objects의 수: n, k-dimension이 독립 e.g) 나이, 연봉
dimension의 구간: ∮개 - data는∮^ k 개 조합이 가능해짐.
독립이므로 ∮^ k 개 조합 안에 균등하게 분포되어있지 않음. → ∮^ k 각각에는 data가 몇 개씩 있을까? - ∮^ k 개 조합 중 한 조합에 있는 있는 data의 수:

e.g.) data object 100개 있는 곳에서 dimension이 독립이며 4개이고, 각 dimension을 빈도가 같게 3개의 구간으로 나눔.
그러면 3^4개의 조합이 가능해짐. → 3^4개의 조합 중 한 조합 에 있는 data의 수는 100/81개 이다.
- 표준 편차:
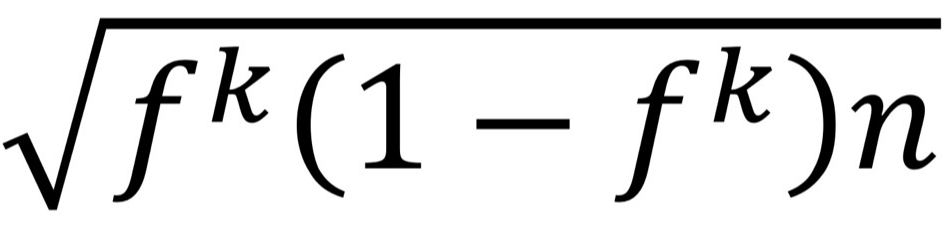
- S(C): 희소성 계수. 한 조합에 나타나는 data object가 얼마나 희소한지, 밀도가 높은지 측정
- n(C): 하나의 조합에 나타나는 실제 data object 수

- S(C)<0 인 경우: 해당 조합(Grid) outlier에 해당,
- S(C)가 너무 큰 경우에도 outlier에 해당. (threshold가 있을 것)
<Ensemble Outlier Detection>
- 여러 Classifier의 결과를 보고, 다수결로 최종 결과 나타냄.
1. dimension의 일부를 추출한 것(서로 다른 subspace)을 여러 개 만듦.
2. 각 sampling의 normal vs outlier의 판정을 진행
3. 더 많은 결과를 voting해서 마지막 결과 출력
- dimension을 sampling 하는 기준
- Feature bagging: dimension 일부를 선택, orginal data를 건드리지 않는 sampling
- Rotated bagging: 기존 dimension의 축을 찾고, k개의 dimension을 잘 설명할 수 있는 축으로 define함. data를 잘 볼 수 있는 축으로 rotate함. rotate한 상태에서 subspace 추출해냄. original data가 축에 해당하는 값으로 바뀜.
값 바뀌므로 numeric data에서만 사용 가능
- voting 방식: 평균 계산, max 선택
- normalization이 중요하게 됨. (서로 값의 범위가 다르면 어려워짐)
<Outlier detection의 딥러닝>
- high-dimension에 대한 처리 매우 good.
- embedding(벡터): row data에서 embedding이 뽑혀져 나옴. dimension이 조금 축소되어서 나오지만,
semantical(의미적) 해석이 들어간 압축. - row data보다 embedding을 썼을 때 결과가 훨씬 더 좋아지길 기대
- 고전적 방법: embedding으로 전처리 하고, 그 다음부터 고전적인 outlier detection 진행
<High-Dimensional Outlier 모델링하기>
- data들이 가까이 있을 때(outlier가 아닐 때)→ data 사이 끼인 각이 넓음, variance (값) 큼 (모든 data 볼 때 많이 움직여야 함)
- outlier면 → 사이 끼인 각이 좁음, variance(값) 작음 (모든 data 볼 때 조금 움직여도 됨)
- 똑같은 각이어도 거리가 멀면 variance 작아지므로 거리에 대한 보정 필요 (분모가 제곱이 되게 거리 한 번 더 나눠준 이유)
- ABOF(o) (variance, 값) 작을 수록 outlier

