<선형(Linear) 회귀>
- 선형 회귀: 입력 데이터를 가장 잘 설명하는 기울기와 절편값을 찾는 문제 (최적화된 직선을 찾는 문제)
- 선형 회귀의 기본식(직선의 방정식): f(x)=Wx+b
- 기울기: 가중치 W
- 절편: 편향 b - 비선형 회귀: 곡선을 찾는 문제
- 학습 데이터를 선형 회귀 모델에 넣으면 예측값을 출력

- 단순 선형 회귀
- 특징 x가 하나인 선형 회귀
- W와 b:정확한 예측을 위해 알고리즘이 '학습'하려고 시도하는 매개 변수
- x와 y는 학습 데이터를 나타내고, f(x)는 우리의 예측을 나타냄 - f(x) = wx + b
- 다중 선형 회귀
- 특징이 여러 개인 복잡한 다중 선형 모델
- w1, w2, w3: 계수, 가중치를 나타냄, 모델이 학습하려고 하는 매개 변수 (차원) - f(x) = w1x1+w2x2+w3x3+...+wdxd+b
<회귀선>
- 데이터에 가장 적합한 직선 → 데이터와 회귀선 간의 간격을 통해 찾을 수 있음
- 각 데이터 포인터에서 직선까지의 거리 계산해 가장 거리가 가까운 직선 찾기 → 오차가 가장 적은 회귀선 찾을 수 있음
- 거리=오차 (error)
- 각 오차를 모두 합하면 오차 총합으로 오차의 크기 따질 수 있음

- 오른쪽: 데이터를 대표하는 직선이 될 수 없음 / 왼쪽: 데이터를 대표하는 직선이 될 수 있음
<손실 함수(Loss function)>
- 위와 같은 회귀선을 찾기 위해 손실 함수(Loss Function)을 활용할 수 있음
- 손실 함수(비용 함수): 회귀선과 데이터 사이의 간격을 제곱하여 합한 값
- 왜 제곱을 하는가?: 회귀선보다 데이터 값이 작으면 차가 음수가 나올 수 있음(오차 제대로 표현 위해)
- n으로 나누는 이유: 오차의 평균값 구하기 위해
- n: 데이터의 개수, f(x): 회귀선의 값, y: 실제 데이터 값

- argmin Loss(W, b): 오차들의 총합을 최소화 시키는 W, b를 찾겠다는 뜻
- 손실 함수는 머신러닝에서 모델의 예측값과 실제값 간의 차이(오차)를 수치화하여 1. 모델의 성능 평가, 2. 개선 방향을 제시
<손실 함수 최소화 기법: 1. 최소 제곱법>
- 최소 제곱법: 손실 함수(평균제곱오차)를 수학적으로 풀어 최적의 해를 직접 계산하는 방식
- 데이터가 적고 차원이 낮을 때 빠르게 계산 가능
- 데이터 많고 차원이 높을 때는 계산 복잡도가 급격히 올라가 비효율적이게 됨
- x: 입력 데이터의 값, y: 목표값



<손실 함수 최소화 기법: 2. 경사 하강법>
- 경사 하강법: 손실 함수의 기울기(그레디언트)를 따라 조금씩(점진적으로) 내려가는 반복적 최적화 기법
- (초기 값에서 출발해 손실 함수를 점진적으로 줄여나가면서 가장 경사가 급한 아래 방향으로 계속 이동하여 최적의 해를 찾음)
- 연속적인 가중치 공간에서 매개 변수를 점진적으로 수행해가면서 최솟값 탐색
- 정확한 해를 찾는 대신 근사적인 해를 찾는 과정 → 수렴 속도와 학습률 조정이 중요
- w: 손실 함수의 값, E(w):손실 함수의 크기, E(w)가 가장 작은 지점에서의 W와 b를 찾음

- 손실함수에 대해 편미분을 함. 손실함수에 대한 기울기 찾음.
- 편미분을 하는 이유:
- 알파: 학습률(움직이는 범위 조절)
- 알파 뒤 식: 기울기
- 양수인지 음수인지에 따라 어떤 방향으로 가야할지 결정 (오른쪽 기울기처럼 기울기가 양수면 아래쪽으로 이동)

- 학습률(learning rate)
- 알파는 한 번에 매개 변수를 얼마나 변경하는지에 관한 비율, 중요한 초매개변수(hyperparameter)
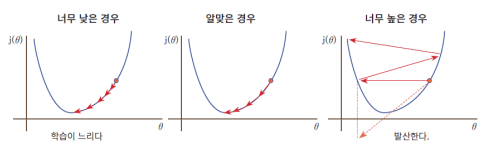
- 학습률이 크면 각 업데이트마다 큰 폭으로 이동 → 초기 단계에 빠르게 손실 함수가 감소하면서 최적의 해에 가까워질 ㅜㅅ 있음
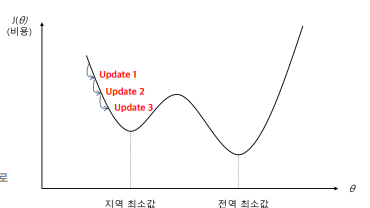
- 학습률이 작으면 최적해에 도달하는 데 매우 오랜 시간이 걸릴 수 있음, 때로는 국소 최적해에 갇혀 전체 최적해에 도달하지 못할 가능성도 있음
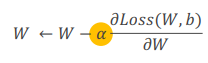

<학습과 매개 변수>
- 에폭(epoch): 모델이 학습을 위해 전체 데이터셋을 반복해서 학습하는 횟수 (몇번)
- 학습률과 함께 매개변수를 찾는 데 중요한 역할을 하는 초매개변수
- 에폭 높을 때: 모델이 데이터를 여러번 학습해 더 정교한 학습 가능, but 학습 길어지고 과적합 발생
- 에폭 적을 때: 과적합 위험 낮출 수 있지만, 모델을 충분히 학습하기 못해 성능이 낮아지는 과소적합 문제 발생
- 현재 배치 경사 하강법에서는 에폭을 기준으로 매개변수를 업데이터 but 다른 경사하강법에서는 배치 크기를 조절해 각 배치에 따라 매개변수를 업데이트 하는 경우 있음
<모델 평가 및 성능 측정>
- MSE(평균 제곱 오차) : 해당 모델의 예측 정확도(해당 모델의 예측 정확도)
- 실제 값에서 예측값을 뺀 제곱 평균 (실제 값의 분산의 평균)
- 일반적으로 선형회귀에서 손실함수로 MSE를 사용, 모델 성능 평가에도 사용됨
- 제곱값이기 때문에 예측값과 단위 다름, 1 미만의 오차는 더 작게, 1 이상의 오차는 더 크게 측정되는 문제
→ 이상치가 많이 존재한다면, 성능을 과대평가할 가능성이 있기에 루트를 씌운 MSE, RMSE도 많이 활용함
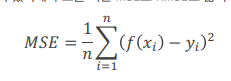
- R^2 (평균 제곱 오차, Mean Squared Error): 해당 모델의 설명력(데이터의 변동성 설명)
- 예측값의 분산을 실제값의 분산으로 나눈 것
- 전체 변동 중 회귀식이 해당 x와 y의 관계를 설명할 수 있는 정도
- 1에 가까워질수록 성능이 좋은 모델
- 다만, 일반 R^2값은 특징 수가 많아지면 자연히 늘어나는 특징이 있기 떄문에, 특징 수가 많을 때에는 Adjusted R^2 사용
- 어떤 x들이 어떤 y를 만드는지 평가할 수 있음
- R: 특징의 개수
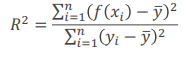
<모델 성능 개선 방법>
- 좋은 것: 데이터가 많은 것
- 데이터에서 어떤 전처리 방법 쓰는지가 매우 중요
- 모델 성능 이전에 데이터 전처리가 잘 이루어져야 함
- 추가 데이터 수집
모델 성능을 개선하는 가장 좋은 방법 중 하나 외부데이터를 보강하거나 이전에 고려하지 않았던 데이터를 추가해 모델 개발에 더 많은 데이터 활용 - 추가적 데이터 전처리
결측치 처리, 범주형 데이터 인코딩 등 각종 데이터 전처리 기술을 적용해 모델이 데이터에서 특징을 잘 포착할 수 있도록 추가적 전처리를 수행할 수 있음 - 데이터에서 다른 특징 선택
데이터셋의 다른 특징이 목푯값을 예측하는데 더 적합할 수 있음. 그래서 다른 특징들이 목푯값에 미치는 영향에 대해 탐색적으로 분석을 하여, 적합한 특징은 선택, 부적합한 특징은 제거하는 방식으로 모델 성능 높임 - 다른 알고리즘으로 모델 훈련
때로는 선택한 알고리즘이 해결하려는 문제나 데이터 특성에 적합하지 않을 수 있음(단순 or 복잡 or 특수). 이럴 때에는 아예 다른 알고리즘을 활용해 모델을 훈련하는 것이 적합함.